Geometric Sequence and Series
This article explores geometric sequences and series. It covers how to recognise a geometric sequence and series, finding common ratio, calculating the nth term of a geometric sequence, finding the sum of a geometric series, solving problems involving growth and decay and finding the sum to infinity of a convergent geometric series, solving problems involving growth and decay and finding the sum to infinity of a convergent geometric series.
Geometric series: Is a series with a constant ratio between successive terms. Each successive term can be obtained by multiplying the previous term by the constant ratio
In a geometric sequence we get from one term to the next by multiplying by the same number each time. We call this number the common ratio r, below are some examples of geometric sequences.

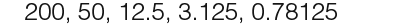
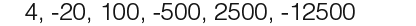
In the following examples we shall explore working with geometric sequences.
In the following examples we shall explore working with geometric sequences.
Finding the common ratio
The following example explores finding the common ratio
Example: Find the common ratio in the following geometric sequences;

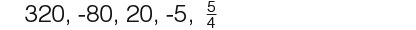
Answer
Explanation: First let us work with the sequence;

To identify each team in the sequence we’re going t o use U1, U2, U3 etc. We know that U1 = 4, U2 = 20, U3 = 100. To work out the common ratio we divide the following term by the previous term ie.

For the sequence above the common ratio is;

The next sequence was;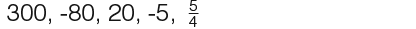
The same principal applies. To find the common ratio we use;

Plug in the numbers as shown below;
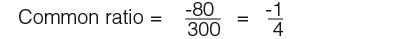
To identify each team in the sequence we’re going t o use U1, U2, U3 etc. We know that U1 = 4, U2 = 20, U3 = 100. To work out the common ratio we divide the following term by the previous term ie.
For the sequence above the common ratio is;
The next sequence was;
The same principal applies. To find the common ratio we use;
Plug in the numbers as shown below;
Note that a common ratio can be a negative number or a fraction/decimal number.
The following shows how to define a geometric sequence note that the first term is a and r is the common ration.
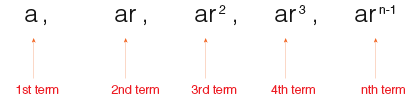
The geometric sequence is also often referred to as a geometric progression.
Above we have formed a formula for finding the nth term;

The following shows how to define a geometric sequence note that the first term is a and r is the common ration.

The geometric sequence is also often referred to as a geometric progression.
Above we have formed a formula for finding the nth term;

Finding the nth terms
Example
Answer
Explanation
Find the 10th and nth terms in the sequence;

Let us start with the first sequence.

For the above sequence we know that a = 3 and the common ratio r is;
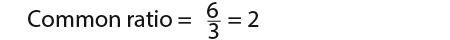
To find the 10th term we use the formula described above so that;
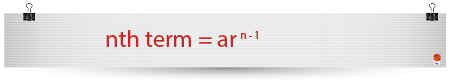
We know n = 10, a=3, and r=2 so;
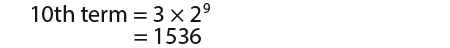

Next we shall look at the next sequence shown below;

Again here to find the 10th term we use the formula …we know that for the sequence a=40, r= -½ and n=10, so we get
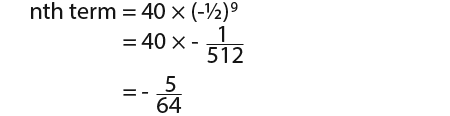
Again to find the nth term formula we use what we know to get;

Here are more examples involving geometric sequences; Suppose a positive geometric sequence is 4 and the 4th term is 8. What is the common ratio and the first and 10th terms.
First let us find the common ratio, we use what we know; we know that;
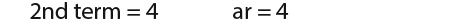
…and the…

…if we divide both expressions to get;

So the common ratio is √2.
Next we shall find the first term. We can use the common ratio found above so we substitute in one of the equations above since a represents the first term.

Next we shall find the 10th term. We can use the geometric sequence formula; we know a=2√2, r=√2 and n=10, therefore;
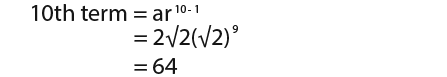
…therefore the 10th term is 64.
Find the 10th and nth terms in the sequence;

Let us start with the first sequence.
For the above sequence we know that a = 3 and the common ratio r is;
To find the 10th term we use the formula described above so that;
We know n = 10, a=3, and r=2 so;
Next we shall look at the next sequence shown below;
Again here to find the 10th term we use the formula …we know that for the sequence a=40, r= -½ and n=10, so we get
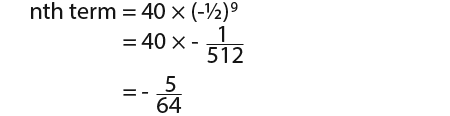
Again to find the nth term formula we use what we know to get;
Here are more examples involving geometric sequences; Suppose a positive geometric sequence is 4 and the 4th term is 8. What is the common ratio and the first and 10th terms.
First let us find the common ratio, we use what we know; we know that;
…and the…
…if we divide both expressions to get;

So the common ratio is √2.
Next we shall find the first term. We can use the common ratio found above so we substitute in one of the equations above since a represents the first term.

Next we shall find the 10th term. We can use the geometric sequence formula; we know a=2√2, r=√2 and n=10, therefore;
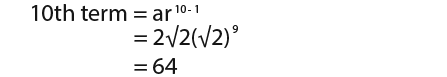
…therefore the 10th term is 64.
Working geometric sequences
ExampleThe numbers 3, x, and (x + 6) form the first three terms of the geometric sequence. Find the possible values of x and the 10th term of the sequence;
Answer
ExplanationFirst let us find the possible values of x. We know that;

This is the common ratio if it is a geometric sequence so we have;

…simplify to get…

…simplify further to get;

…we need to solve to find x, factorise to get;

…since the sequence contain only positive numbers we shall accept x=6.
Next we shall find the 10th term, …simply we use the formulas;
…we know that r=2, a=3 and n=10, so we get;
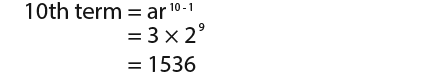
…therefore the 10th term is 1536.
This is the common ratio if it is a geometric sequence so we have;
…simplify to get…
…simplify further to get;
…we need to solve to find x, factorise to get;
…since the sequence contain only positive numbers we shall accept x=6.
Next we shall find the 10th term, …simply we use the formulas;
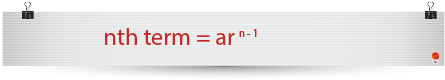
…we know that r=2, a=3 and n=10, so we get;
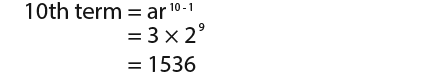
…therefore the 10th term is 1536.
Geometric sequence can also be used to solve problems involving growth and decay, for example interest rates population growth and decline.
ExampleAnthony invests £A at a rate of interest 4% per annum. After 5 years it will be worth £20,000. How much will it be worth after 10 years.
Answer
ExplanationIf the total increases by 4% each year from the previous year that must mean that every year the total will 100% from the previous year plus 4%, therefore.

Converting that into decimals gives.

That means we will use the multiplication factor 1.04 after each year for the rise. After the first year the investment is worth;

…and after 2 years it will be worth.
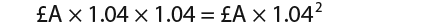
It is therefore logical to conclude that after 5 years the investment will be worth;

The above expression is a geometric sequence formula where a =£A and r=1.04.
Above it is written that investment is worth £20,000, we can use this with the formula to find the initial investment; We form an expression like this;

…therefore;
So the initial investment was £16438.54.
We can use this to work out what the investment will be worth after 10 years; …we simply substitute A in the equation;
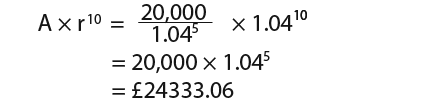
So the investment will be worth £ 24333.06.
Converting that into decimals gives.
That means we will use the multiplication factor 1.04 after each year for the rise. After the first year the investment is worth;
…and after 2 years it will be worth.
It is therefore logical to conclude that after 5 years the investment will be worth;
The above expression is a geometric sequence formula where a =£A and r=1.04.
Above it is written that investment is worth £20,000, we can use this with the formula to find the initial investment; We form an expression like this;
…therefore;

So the initial investment was £16438.54.
We can use this to work out what the investment will be worth after 10 years; …we simply substitute A in the equation;
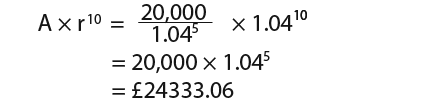
So the investment will be worth £ 24333.06.
Inequalities
Example: what is the first term in the geometric progression 3, 6, 12, 24, to exceed 1 million.
Answer
Explanation
This example involves inequalities we can use the nth term formula;
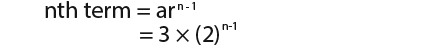
We want the nth term to be greater than 1 million that is;

…therefore…

…we simplify;

…we must use logs here to solve n;
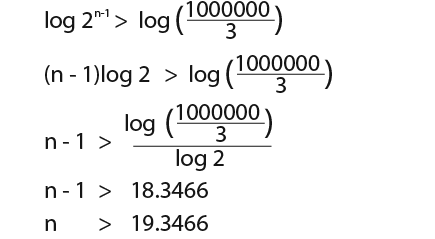 <
…therefore n is 20 which represents the 10th term the first to exceed 1000000.
<
…therefore n is 20 which represents the 10th term the first to exceed 1000000.
This example involves inequalities we can use the nth term formula;
We want the nth term to be greater than 1 million that is;
…therefore…
…we simplify;
…we must use logs here to solve n;
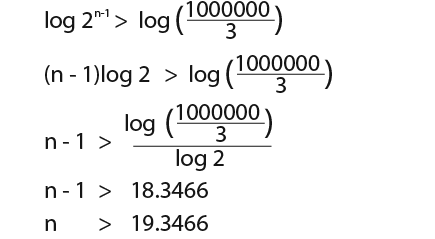 <
…therefore n is 20 which represents the 10th term the first to exceed 1000000.
<
…therefore n is 20 which represents the 10th term the first to exceed 1000000.
Sum of geometric sequences
The following examples explore finding the sum of a geometric series;
We know that the general form for the geometric sequence is a, ar, ar2, …, arn, therefore the sum;

…multiplying the series above by r to get;

…now we can subtract rSn from Sn

…therefore;
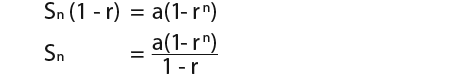
The general rule for the sum of a geometric series is;
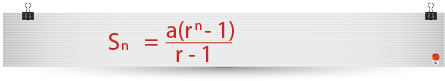
…or…
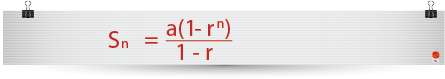
We shall use the formula in the following example;
We know that the general form for the geometric sequence is a, ar, ar2, …, arn, therefore the sum;
…multiplying the series above by r to get;
…now we can subtract rSn from Sn
…therefore;
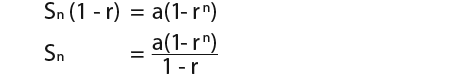
The general rule for the sum of a geometric series is;
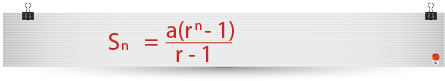
…or…
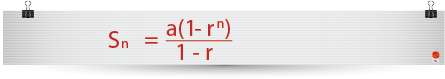
We shall use the formula in the following example;
ExampleFind the sum of the following series;
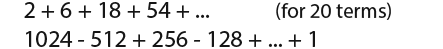
Answer
Explanation
For the first series;

…we have to find up to 20 terms, we know that a=2, r-3 and n=20, because r=3 is greater than 1. We shall use the formula;
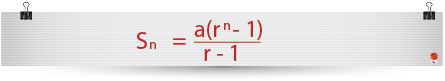
For the next series we will have to find the position of the last term;

…we know that a=1024 and r= -½ when nth term = 1

…we solve to find n

…because (-2)n-1 = (-1)n-1(2n-1) = 1024, that must mean that; (-1)n-1 must be positive and…

…now we can use logs to solve n;
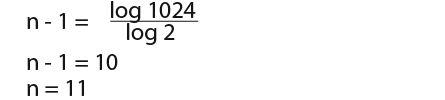
Now we can find the sum of the series according to n=11. Because r=-½ is less than 1 we use the formula;
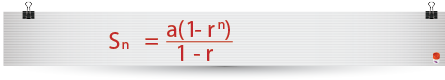
…so we have;
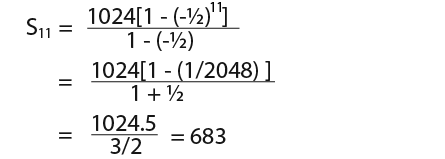
For the first series;
…we have to find up to 20 terms, we know that a=2, r-3 and n=20, because r=3 is greater than 1. We shall use the formula;
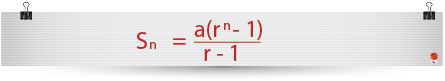
For the next series we will have to find the position of the last term;
…we know that a=1024 and r= -½ when nth term = 1
…we solve to find n
…because (-2)n-1 = (-1)n-1(2n-1) = 1024, that must mean that; (-1)n-1 must be positive and…
…now we can use logs to solve n;
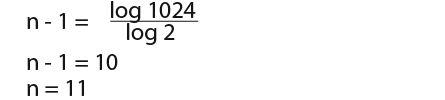
Now we can find the sum of the series according to n=11. Because r=-½ is less than 1 we use the formula;
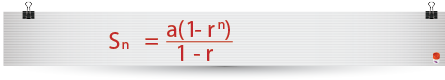
…so we have;
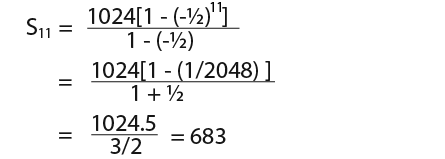
Example: An investor invests £4000 on January 1st every year in a savings account that guarantees him 4% per annum for life. If interest is calculated on the 31st of December each year, how much will be in the account at the end of the 10th year?
Answer
Explanation: Be careful here with the question. The investor invests £4000 every new year and the total amount for each year is calculated on the 31st of Decemeber.
By now we know that a rate of 4% means x1.04. At the end of year 1, the amount is;

at the start of year 2 the amount is;
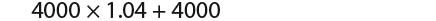
…notice that we have added the new investment at the end and at the end of year 2 the amount is;
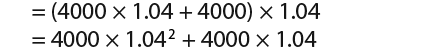
…notice that at the end of each year the total amount is multiplied by 1.04.
At the start of year 3 the amount;
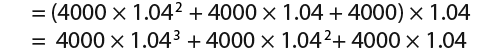
…that must mean that at the end of year 10, the amount is;
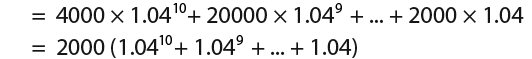
The part in brackets above is a geometric series and therefore we can use the formula for it;

…we know that a=1.04, r=1.04 and n=10, therefore;
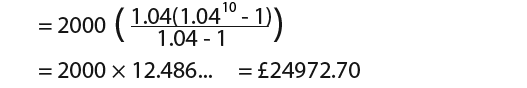
By now we know that a rate of 4% means x1.04. At the end of year 1, the amount is;
at the start of year 2 the amount is;
…notice that we have added the new investment at the end and at the end of year 2 the amount is;
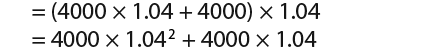
…notice that at the end of each year the total amount is multiplied by 1.04.
At the start of year 3 the amount;
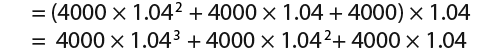
…that must mean that at the end of year 10, the amount is;
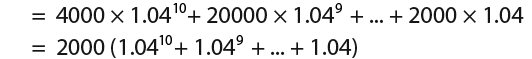
The part in brackets above is a geometric series and therefore we can use the formula for it;

…we know that a=1.04, r=1.04 and n=10, therefore;
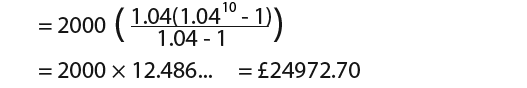
Example: Find the least value of n such that the sum of 1+2+4+8+… to n terms would exceed 2000000.
Answer
Explanation: …we know that a=1, r=2, we can substitute this into the formula;
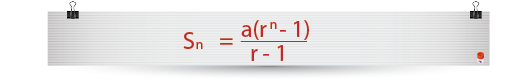
…therefore the sum to nth terms is;

…the inequality we’re after is;



…we can now use logs to find the value of n;
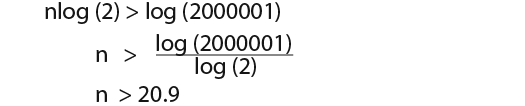
…we can conclude that the sum of the series needs 21 terms for it to exceed 2000000.
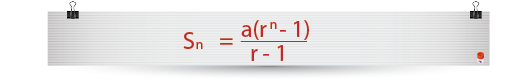
…therefore the sum to nth terms is;

…the inequality we’re after is;
…we can now use logs to find the value of n;
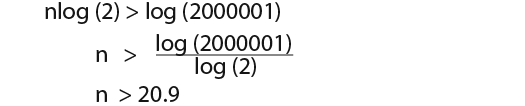
…we can conclude that the sum of the series needs 21 terms for it to exceed 2000000.
Click here to continue to geometric series sum to infinity.
