Rates of Change

Sometimes we want to know how things change over time or how another quantity is changing while another is changing, for example if the radius is changing over time what is the rate of change for the area?

You must have some knowledge of differentiation especially using the chain rule, before continuing with this lesson. There are lot’s of lessons published on this site that you can look at, just look in the Calculus section.

Example

A spherical balloon is being blown using a pump. It has been measured that the radius is increasing at the rate of 4cm per second. How fast is the volume increasing when the radius is 8 cm?

We know that the balloon’s radius is increasing at the rate of 4cm per second.

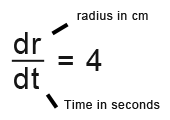
We’re being asked for the rate of change of volume;

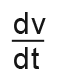
Using the chain rule;

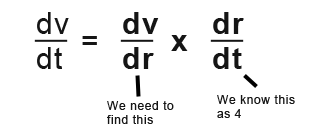
Now we need to find the differentiation of volume dv/dr
We know that the formula for the volume of a sphere is;

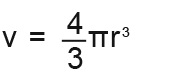
We need to differentiate that;

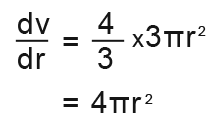
So our rate of change of volume becomes;

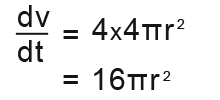
The rate of change of volume at time t is 16πr² When the balloon is 8cm in radius the rate of volume is;

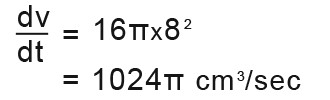
The answer to the rate of change of volume is 1024π cm³/sec.

Example 2

A water tank has a shape of a prism with base of 2m and 3m. The tank is being filled with water at the rate of 0.3m³ per minute. At what rate is the height of the water increasing?

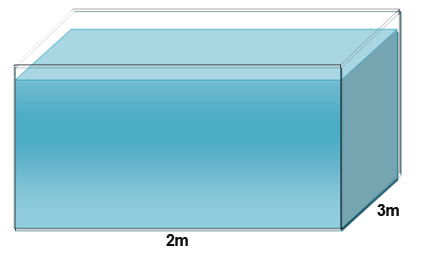
We know that the volume is increasing at the rate of 0.3m³ per minute, this can be expressed as;

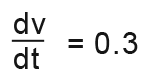
We want to find the rate of change of the height;

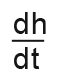
You can find this using the chain rule;

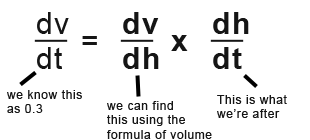
We don’t know dv/dh so we need to find it. We know the formula for the prism is v = wlh so;

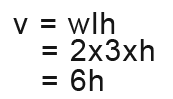
We differentiate the volume’

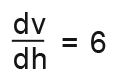
Now we have all the values, we just need to substitute to find what we don’t have;

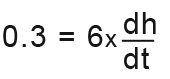
We want the rate of the height over time as shown in the above expression, so we rearrange as;

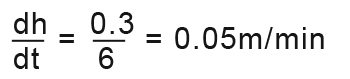
The height of water is increasing at the rate of 0.05m/minute

And that is how you work with rates of change. Remember to identify what is required and what you have. In most cases you will be required to use a formula and then differentiate it and multiply it with what rate you have (Chain rule) and finally substitute in the given value. This is usually the procedure. It’s that simple.