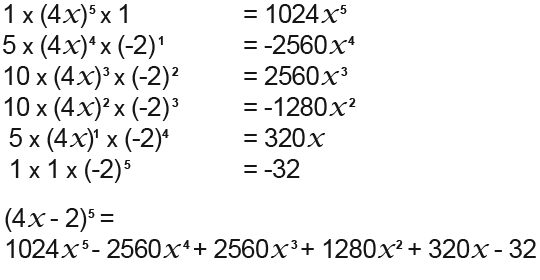Pascal’s Triangle

Expanding very large powered numbers can be quite tedious, since the expansion requires a lot of expanding over and over again. For example trying to expand (x+1)⁵ and (x+1)⁷, this would take a very long time and cause lot’s of headaches to work.
For such numbers we can use the Pascal’s triangle to simplify the all process. The Pascal’s triangle was named after a mathematician called Blaise Pascal (1623-1662). Let us try to expand powers from one upwards and see whether we can note a pattern.

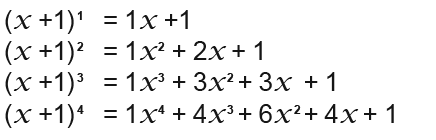
If you look careful at the above work outs you might be able to note a pattern. You can see that the numbers of terms increase as the powers increase, also a trying is visible or formed.
Let us look at the expansions again but this time the coefficients in different colours;


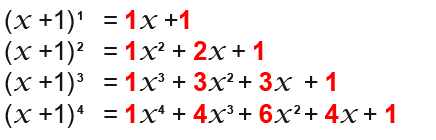
From the above this is how the Pascal’s triangle is formed;

If you look carefully at this triangle of numbers you will note that each number in each row is found by adding together two numbers above it. For example for the next row, the number below 1 and 4 is 4+1=5 and so on. So the 5th row numbers become; 1, 5, 10, 10, 5, 1 as shown in the following Pascal’s triangle.

So the power 5 expansion becomes;

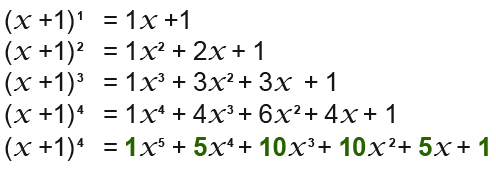
We can use Pascal’s triangle to carry out any expansion for example (a+b)⁵. We need to work out the coefficients of the terms in the expansion; these coefficients can be found in the fifth row of Pascal’s triangle. The fifth row numbers are; 1, 5, 10, 10, 5, 1, so now we can fill in the a terms as follows;

Note that we’re adding in the a terms starting with the highest power then going down until power one, then we add the last number (1) in the fifth row of the Pascal’s triangle.
Next we need to fill in the b terms, these go up instead of down opposite to the a terms, so the final becomes;

So;

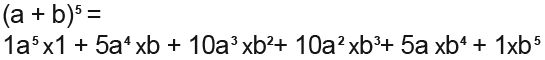
These are the rules to note while using the Pascal’s triangle referencing to the above;

Example

Here is an example we could expand; (4x – 2)⁵
We need to find out the numbers of the fifth row in Pascal’s triangle. Then we fill in the 4x as a and the -2 as b. This has been shown below;