Quadratic Formula

Using the quadratic formula is one way of solving quadratic equations. Another way of solving quadratic equations is by factorising or factorisation. It is very important in this lesson to be able to solve quadratic equations through factorising. This is a good lesson on how to do that [LINK IS MISSING]. This is the quadratic formula.

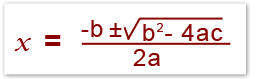
The quadratic formula becomes useful when trying to solve quadratic equations which cannot be solved through factorising. Take for example;

This cannot be solved by factorising. When the quadratic formula is used the result from it is two values for x when the equation is equal to zero. The quadratic formula is used to solve equations of the form ax²+bx+c=0 where the letters are the coefficients of the terms in the equations. For example the equation 4x²-x-8=0; a=4, b=-1 and c=-8.

Example

Solve the equation; 3x²+5x+2=0.
First we need to find the values of a, b, c to use in the quadratic formula.

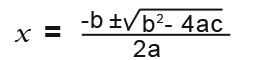
Here a=3, b=5 and c=2.
So we substitute the values of a, b, c into the formula to get;

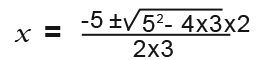
We need to simplify the formula 5²=25, 4x3x3=24, and 2×3=6 so the result becomes;

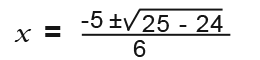
We simplify further…

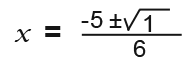
The ± means add or subtract (+ or -) so the first x or the first solution is;

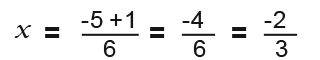
The second solution we subtract instead so;

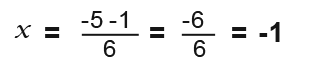
So the second solution or x is -1.
The final answer becomes;

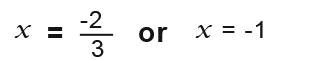
And that’s how you work with the quadratic formula.