Intersecting Lines

For this learning tutorial you must have some basic knowledge of graphs. You must also be able to draw graphs. You must also know how to solve simultaneous equations.
In this lesson we shall be finding out the point on the graph where lines on the graph intersect.
You must know that lines which are parallel will never meet or intersect each other, therefore any lines on the graph that are not parallel will meet each other at some point.
One way of finding where two lines intersect on the graph is by reading off the graph. Although this is a quick way to do that, it’s impossible to be accurate especially when the lines meet at decimal numbers. Also lines which meet at very large coordinates can sometimes be impossible to drawn on the graph, imagine drawing a point at the coordinate (1000, 2893). The following graph shows an example of two lines which intersect.

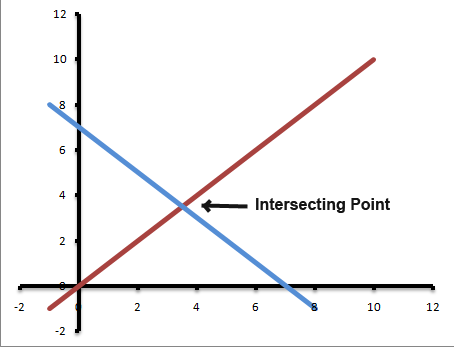
We can find the point where the two lines meet more accurately by using simultaneous equations.

For example

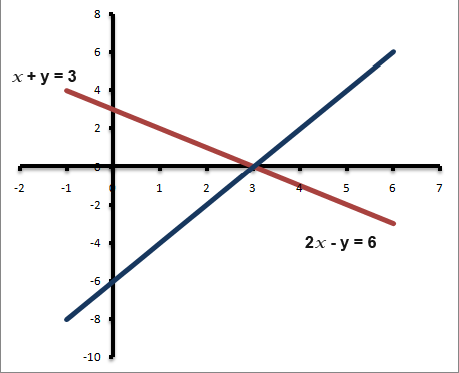
Find the point where the following two lines intersect; x+y=3 and 2x-y=6.
This first example is the much simpler version. We need to fine the values of x and y, to do that we need to get rid of one of the equations and the terms (for example y). We do this by adding the equations together, so;

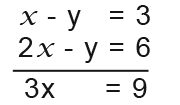
Notice we’ve got rid of y and the term with x in it remains. Here;

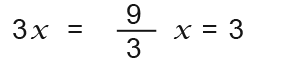
Now we substitute the value of x we’ve found into one of the simultaneous equations to find the y value.

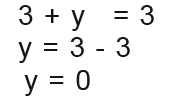
The line must intersect at (3, 0). We can see this point on the graph below.

Example 2

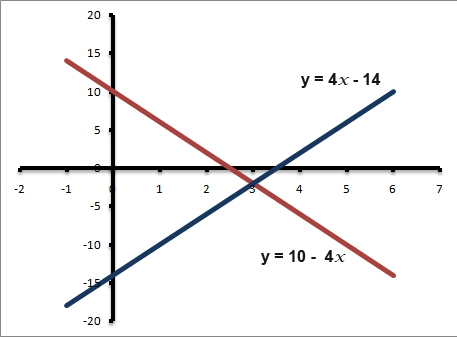
Find the point where the following lines intersect; y=10-4x and y=4x-14
There are two ways we’re going to explore that will enable us to find out the point where these two lines intersect. One of these ways you will probably use regularly as it’s simple and straight forward. Let’s start with the simultaneous way first.

Method one

When you look at these equations you will see that they both have y as the subject. We shall first rearrange them to resemble the ones we had in the first example; that is move all the terms with letters to one side and the numbers to the other. The result;

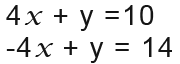
Now we need to subtract and solve the equations;

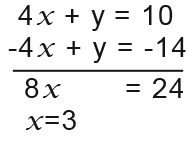
To find the y-coordinate we simply substitute 3 (the x value) into one of the equations.

So the point of intersection is (3, -2).

Method two

This next method is simple and straight forward you will probably use it often;
For the both lines to intersect, both values of y must equal meaning that;

…Very simply the lines will intersect at the same y coordinate. And this is true, you must try to understand that so take some time to think about it. Now we solve by rearranging and finding the x value of the coordinate where both lines intersect.

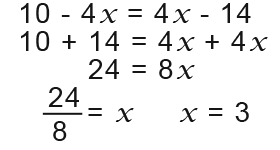
Now use one of the equations to find y.

The coordinate of intersection is (3, -2).
This is the same answer as we got in method one of this example. The following graph shows the two lines and the point of intersection.

Example 3

Find the point where the following lines intersect using substitution; y=3x+5 and 2x-3y=6.
In this example I am introducing a new method. This method is not tricky at all; it’s very logical and straight forward. You might have realised this in the previous examples.
We know what y is in the first equation; y=3x+5. So to get rid of y, this is what we have been doing all this time. We replace the letter y in the second equation with that of the first equation and the result is;

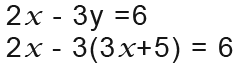
Now we expand the brackets and solve the equation.

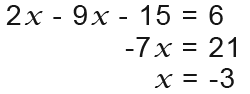
So now we know the value of the x coordinate on the graph, we just simply use one of the equations in question to find the y coordinate.

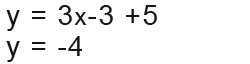
And the point of intersection for the lines y=3x+5 and 2x-3y=6 is (-3, -4).
The following graph shows these two lines and the point on intersection.

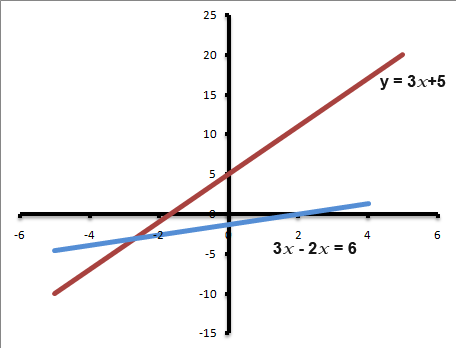
Example 5

Find the point where the following lines intersect; y=3x+5 and 2x-3y=6
This example involves the same equation as the ones in question 4. First we will need to first rearrange all the equations into the form ax+by=c

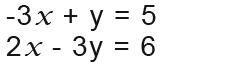
In order to subtract or add these equations to get rid of the y terms we shall need to make the y terms in both equations equal. We do this by multiplying. We should make the y term in the first equation equal to 3y by multiplying the equation by 3 as follows.

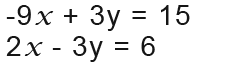
Now we can add the equations to get rid of the y terms;

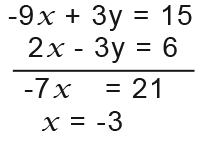
Now we’ve finally found our x coordinate, we need to fine the y coordinate by using one of the equations in question. We substitute -3 (the x value) into y=3x+5 and then solve;

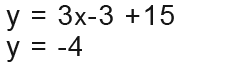
The coordinate becomes (-3, -4) This is where both lines intersect.
And that’s how you find the point where two lines intersect. It’s that simple.