Sine Rule

This chapter covers the sine rule used in trigonometry. We shall be exploring how to use the sine rule to find missing sides and angles. You must have some basic knowledge of trigonometry.
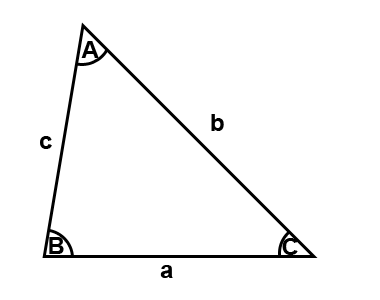
If we know the sides/angles in a triangle we can use the sine rule to find any missing sides/angles in that triangle. Here is a triangle.

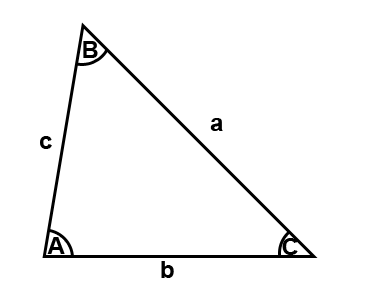
The sine rule formula is;

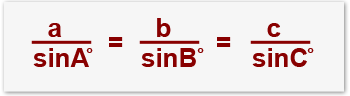
The capitals in the formula represent angles while the lower case letters represent sides.

Finding sides

In the first following examples we shall be looking at how to find the missing sides of a triangle using the sine rule.

Example

Here is an example of how to use the sine rule.
Find the length x.

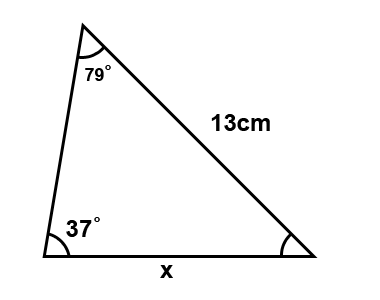
We know the formula for the sine rule. We need to identify what part of the formula we can use as shown below.

Now we substitute in the values as shown below;

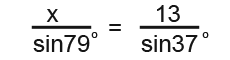
We rearrange the equation to find x.

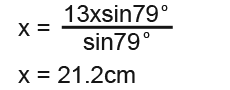
And we have managed to find the value of x as 21.2cm.

Finding angles

Now we shall explore how to find the angles in a triangle using the sine rule.
To find angles in a triangle we need to rearrange the formula first. This is our original sine rule formula.

Now lets’ one part and cross multiply or multiply through by sine x.

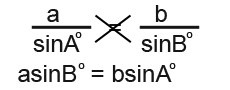
Now we divide through by a and b.

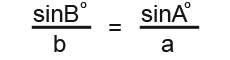
The full formula for finding the angles becomes;


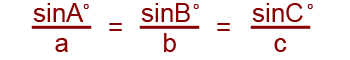
The following is an example of how to use the above formula;

Example

Find the angle θ

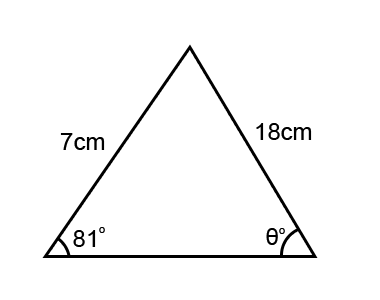
First we substitute in the known values;

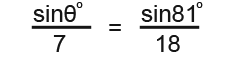
And then we rearrange the formula;

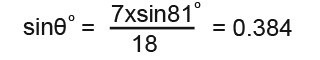
Lastly we need to undo the sine value we have found to find the angle;

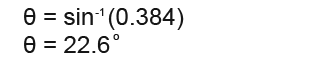
The angle θ is 22.6°

Ambiguous cases

Here is an example of some ambiguous problems that you might encounter.
Find the missing angle A in the following triangle.

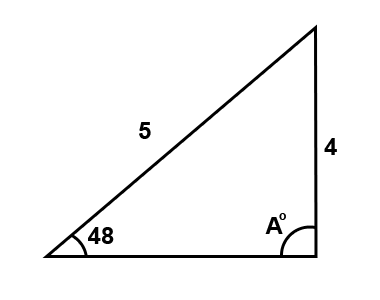
The missing angle in this triangle is an obtuse angle (angle greater than 90°) Lets use the sine rule to find this angle.

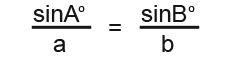
Now substitute in the values to find the angle;

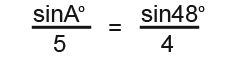
Rearrange and get;

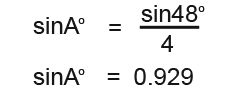
Reverse the sine to find the angle;

That is not the final answer as we’ve found out that this angle must be >90° (greater than 90°) Actually the angle we have found is this angle;

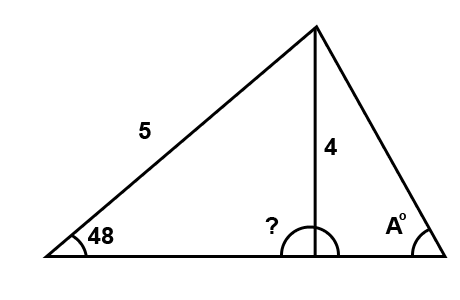
The above triangle has exactly the same lengths and angles as the one drawn below. Looking at the above angle, the angle we want to find is 180° minus the acute angle we have just found using the sine rule.

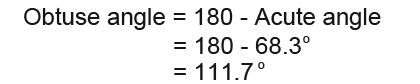
We have managed to solve this ambiguous problem. Watch out as you will find many problems such as this.