Midpoints and Coordinates

In this section we shall be looking at coordinates and midpoints. We shall explore how to read and plot coordinates in all 4 quadrants and look at shapes and pattern in coordinates, work out mid points between pairs of coordinates. You must have some basic knowledge of coordinates to appreciate this entry. Here is a grid shown below.

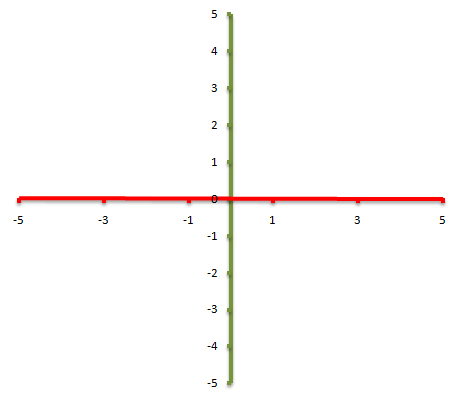
The line in red is called the x-axis while the line in green is called the y-axis. To write the coordinates of any point which lieas on the axis we write the coordinate in the form.
[IMAGE]
The x-axis tells us how many units the point on the axis across and the y-axis tells us how many units the point is on the y-axis (up or down)

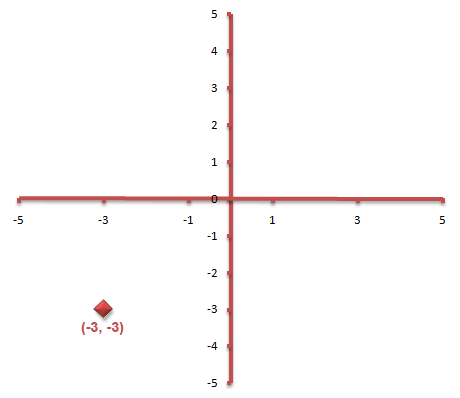
The point shown on the grid is (-3, -3).

Mid points

Suppose we had two points A and B. The label M is a midpoint half way A and B. Suppose we wanted to find the midpoint (M) coordinate.

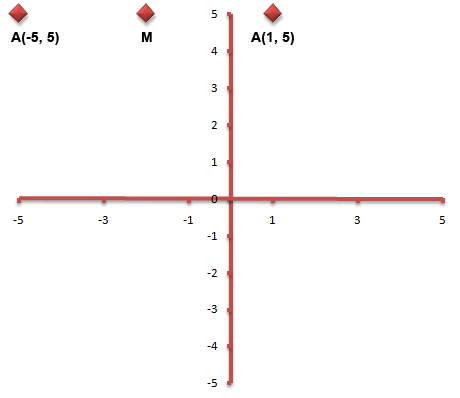
On the grid above we can see that M lies on the same horizontal line with A and B. This means the y-coordinate on M is the same as the other points A and B. This must be a y-coordinate of 4 so;

The x coordinate of M is halfway between -5 and 1. The x coordinate of M must be -2, so the full coordinate of M is;

Diagonal Midpoints

The grid below shows two points A and B. The point M lies between points A and B. Suppose we wanted to find the coordinate of M.

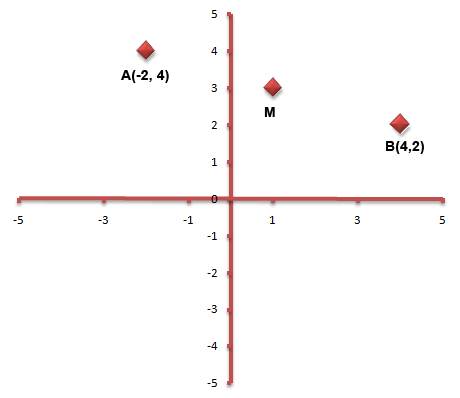
The x coordinate of M is halfway between points A and B between -2 and 4. The coordinate must be 1, so;

The y-coordinate of M is halfway between 4 and 2. The y coordinate of M must be 3. So the full coordinate of M is;

Without Grid

You might sometimes want to find a midpoint without a grid. In the following example we shall be exploring that.

Example

Find the midpoint M between (-7, 6) and (-5, 8)
First we must find the midpoint of the x-coordinate of (-7, 6) and (-5, 8) points. The half way we’re trying to find is between -7 and -5. To find this we add then divide by 2 as shown below.

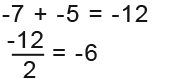
Now we have found that the halfway of -7 and -5 is -6; so our first coordinate of the midpoint is;

To find the midpoint of the y-coordinate we do exactly the same. We add 6 and 8 and then divide 2 as shown below.

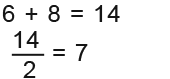
Now we have found that the halfway of 6 and 8, therefore the y-coordinate is 7. The y-coordinate of the midpoint of M is 7. The full coordinate of the midpoint M is;

That concludes the section coordinates and midpoints.