Linear Equations

This is the first entry on equations. In this section we shall be exploring equations at a basic level. This is simply an introduction to linear equations. We shall look at using letters for unknown numbers and solving simple linear equations.
Jane had to buy 30 sodas to serve at a party, after the party 12 sodas remained. How many sodas were drunk at the party?
Well let’s look at this in a very basic example/way. We added 12 to a number to get 30. Right?

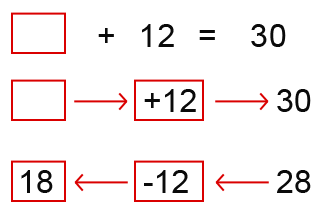
The above diagram shows the value that we need to find. Since we added we must subtract 12 from 30 to find the number that we added. Subtraction is the opposite of addition.

Equations

Above we used a box to represent the number that we were trying to find in our calculation. In algebra we usually represent the numbers we don’t know or unknown values with a letter such as x, y, z, n or any other letter in the alphabet. We could represent the drinks drunk with the letter n as shown below in our calculation.

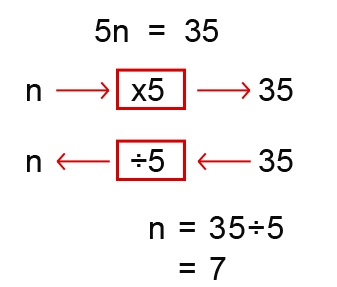
The above expression is called an equation, where we have to find the value of n. To find this value we use a function machine;

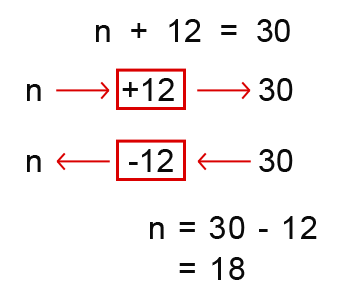
We say that the solution for n is 18. This must be right because;

Solving Equations

The following are some more examples of equations such as we have seen above;

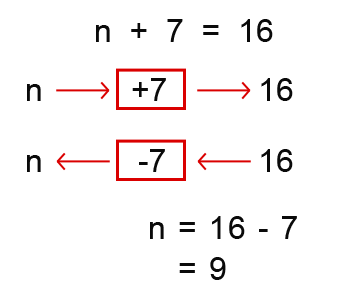
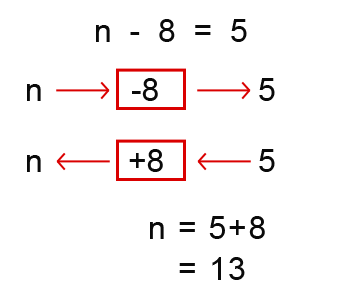
Equations with brackets

You will encounter lots of equations with brackets in maths, for example; Solve (a+4)x8=56
Let’s first hide one part of this equation as shown below;

Suppose we had no idea what was under the hidden area. What value do you think would be there to complete the expression? This must be a 7 because;

This must mean that for out hidden part;
[IMAGE]
We have managed to find the value of a in the original question. Let’s put the value into the original equation to check whether it’s right.

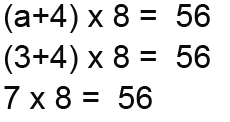
So the value 3 we found was right.
That concludes this entry on linear equations.