Simplifying

This chapter focuses on simplifying expressions. It covers adding together simple lists of letters and numbers including negatives in the list. And lastly multiplying and dividing simple algebraic expressions.
Algebra is a very important branch in mathematics. Technical developments such as computers or gadgets and complex building structures would never have existed without the concepts of Algebra. Algebra relates to real life situations in many ways. Let us look at some basic algebra first.

Rule 1 – Adding letters

We have to find out what a plus a is equal to. a represents an unknown value, we have no idea what that value is. With basic algebra it’s best to describe what you see rather than working out. We’re asked how many as we have and we simply say; “There is 2as” Therefore;

You don’t have to be a wise man/woman to work that out and in most cases in fact all! Algebra is very simple and logical. The above rule works with addition of letters; we simply describe how many letters we have.

Example 2

Here is a second example;

Again here we answer the question be describing what we’re seeing. Here we see;

In algebra we tend to put the letters in alphabetical order. Notice we’ll have done this above. The answer would still be correct otherwise but would be much easier to read if organised in alphabetical order and it also seems right.

Above we have a shape. Suppose we wanted to find the perimeter we have found. We know that the perimeter is the addition of all sides, in this case the perimeter is;

Here we describe what we have as we did above, we have 2a’s and 2b’s thus we write;

Example 3

Suppose the question asked to simplify;

Here we could use our description method. You must remember that numbers on their own cannot be mixed with letters even when they have numbers. Here we collect like terms;

Then we work out to simplify;

…and…

So the answer becomes;

Multiplying and dividing

In this part of the chapter we’re going to be looking at expressions which involve multiplication and division. Simple rules that you must be aware of.

• Anything multiplied by 0 is 0.
  
• Anythings times by 1 is itself.
  
• Multiplying something by itself is called squaring
  
• We never use ‘times by’ signs in algebra because the use of x is popular and this is similar to x which is the multiplication sign

Examples

Suppose the question asked to simplify the following expressions.

Example 1

First we rearrange the expression with the numbers as shown below;

Here we remove the multiplication signs as our next move;

Example 2

Again we carry out the same process here;

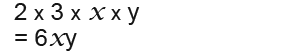
Example 3

First we rearrange and simplify as above;

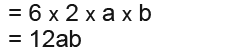
Example 4

Notice this example is quite different from the above and it satisfies the squared rule explored above. First we expand, rearrange and solve.

We know a x a forms a² that must mean;

Division

This part explores division. Suppose we wanted to simplify;

Here we can describe; Halve 6a’s, the half of 6a’s must be 3a’s

Simplify;

We can use the cancelling method here. First we expand the expression as shown below;

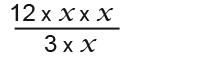
Now we can cancel the top with the bottom. 12 divide by 3 gives 4.

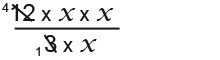
Now we can cancel the x’s

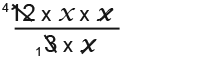
That leaves;

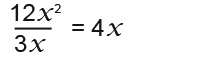
…as the answer.