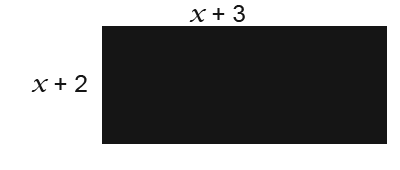Expanding brackets
Rectangle perimeters
Example:The digram below shows a rectangle with 5 units length and 3 units width. Calculate the perimeter of the rectangle.
We could simplify the process and do it quickly by adding up two lots of 5+3 since there are two sides of length and width
The second method is much simpler and better descriptive. We have put 5+3 into brackets and multiplied by 2.
Expressions
Example:Below is a rectangle. Suppose we wanted to find an algebraic expression for the perimeter of the rectangle.
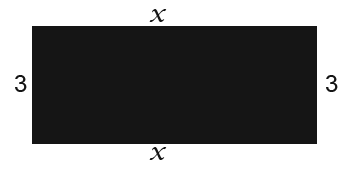
To simplify the all process we simply multiply x+2 by 2 which results in;
If we expand 2(x+3) we get;
That must mean that 2(x+3) is the same as 2x+6.
Squares perimeter
Example:The same applies for squares. Suppose we want to create an expression for the following square.
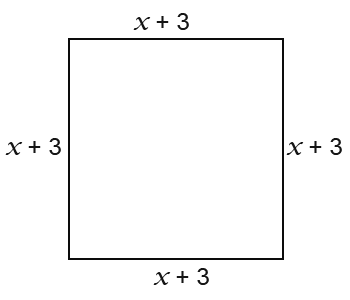
Which we can expand to get;
Then simplify the expression to get;
Foil expanding method
Suppose we wanted to find an expression for the area of the rectangle below;
The sides of the rectangle lengths above have x+3 and x+2. To find the area of a square we multiply the lengths together.
We can get another similar formula if we expand the expression above. The foil method can be very useful in this case.
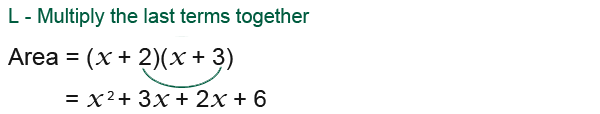
Now we can simplify the expression;
![]()
Expanding x+32
The following tends to be trick to a lot. Suppose we wanted to expand.
![]()
Many happen to solve it like this;
The above is false. Remember that ²/squared means that ‘times by itself’ That must mean that;