Arithmetic sequences
An arithmetic progression or arithmetic sequence is simply a sequence of numbers with a common difference and this common difference has to be constant.
In most cases you will have a set of the first few numbers within a given sequence to observe the progression then easily find out the values of the other nth terms. If you can find the initial term of an arithmetic sequence a1 and the common difference d, then the nth term of the sequence is given by:
And the sum for all the terms in the sequence (sum to nth terms) can be found by:
Example
Find the last term and the sum of 2 + 6 + 10 + 14 + … to 26 terms.
We shall be using the above formulas and we know that d = 4 and a = 2.
Last term
= a + (n – 1)d
= 2 + 25 x 4
=102
Example 2
Find the sum of the first 1000 natural numbers.
The natural numbers are the normal numbers that count 1, 2, 3, 4, …
We know that a=1 and d =1
To find the sum to the 1000 term we use the sum to nth term formula. Let’s first simply the formula before adding the n value ‘1000’
And that’s how you work with arithmetic series or sequences. You can fin any nth term and the sum of the nth terms in the sequence using the above formulas.
________________________________________________________________________________________________________________
Introduction
In this section we will be defining Sequences, Terms, Arithmetic Sequences, Common Differences and Finite Arithmetic Progression. Then we will use examples to show how we find the Common Difference and the nth term.
Quick Summary
• A Sequence is an ordered list of numbers
• A Term is a specific number in a Sequence
• An Arithmetic Sequence is an ordered list of numbers where the difference between the successive terms is constant. We call this constant the Common Difference.
• A finite section of an Arithmetic Sequence is called a Finite Arithmetic Progression (or just an Arithmetic Progression).
We will be using these two formulas in this section:
d = an – an-1
75e8cd43dc5817d40487480b96a07447.png ¬
they will be explained in more detail below.
Finding the Common Difference
As the Common Difference is defined as the difference between the successive terms, we can find the Common Difference by taking a term from our sequence and subtracting the previous one from it:
d = an – an-1
We usual let n=2 i.e.
d = a2 – a1
The behaviour of the arithmetic progression depends on the common difference. If the common difference is: Positive, the members (terms) will grow towards positive infinity. Negative, the members (terms) will grow towards negative infinity.
Example 1
State the first two terms of this Arithmetic Sequence: 7, 15, 23, 31, 39, …
and find the Common Difference
Then state where the members (terms) will grow towards
The initial term a1 = 7 and the 2nd term a2 = 15
Hence d = 15 – 7 = 8. Thus the Common Difference is 8.
As 8 is positive, the members grow towards positive infinity
Example 2
State the first two terms of this sequence 91, 81, 71, 61 …
and find the Common Difference
Then state where the members (terms) will grow towards
The initial term a1 = 91 and the 2nd term a2 = 81
Hence d = 81 – 91 = -10. Thus the Common Difference is -10.
As -10 is negative, the members grow towards negative infinity
Example 3
State the first two terms of this sequence 2.5, 2.25, 2.0, 1.75, 1.5, …
and find the Common Difference
Then state where the members (terms) will grow towards
The initial term a1 = 2.5 and the 2nd term a2 = 2.25
Hence d = 2.25 – 2.5 = -0.25. Thus the common difference is -0.25.
As -0.25 is negative, the members grow towards negative infinity
Example 4
Find the common difference for the Arithmetic Sequence whose formula is
an = 6n + 3
From the question we have
an = 6n + 3
and thus we can see
an-1 = 6(n – 1) + 3
Now we know: d = an – an-1
Hence here
d = 6n + 3 – [ 6(n – 1) + 3 ]
d = 6n + 3 – [ 6n – 6 + 3 ]
d = 6n + 3 – 6n + 6 – 3
d = 6
Thus the Common Difference is 6.
Finding the nth Term
Formula for the nth term of the sequence
Let a1 be the initial term of an Arithmetic Progression and let d be the common difference. Then the formula for the nth term of the sequence (or an) is:
a93173b2cdeea431ce818315ca84ae87.png ¬
More generally, if am is the mth term of the sequence, an can be found using:
1__#$!@%!#__75e8cd43dc5817d40487480b96a07447.png ¬
Example 5
Find the 10th term of the sequence 7, 15, 23, 31, 39, …
From Example 1 we know that the Common Difference = 8 i.e. d = 8.
We can see that a1 = 7, and as the question asks for the 10th term we know n = 10.
Hence using this formula:
1__#$!@%!#__a93173b2cdeea431ce818315ca84ae87.png ¬
We see
a10 = 7 + (10 – 1) x 8 = 79
Example 6
Find the 10th term of the sequence 91, 81, 71, 61 …
From Example 2 we know that the Common Difference = – 10 i.e d = -10.
We can see that a1 = 91 and as the question asks for the 10th term we know n = 10.
Hence using the formula:
2__#$!@%!#__a93173b2cdeea431ce818315ca84ae87.png ¬
We see
a10 = 91 + (10 – 1) x -10 = 1 .
Other Examples
Example 7
Find a formula for the sequence 7, 15, 23, 31, 39, …
From Example 1 we know that the Common Difference = 8 i.e. d = 8 and we can see that a1 = 7. Putting these facts into this formula
3__#$!@%!#__a93173b2cdeea431ce818315ca84ae87.png ¬
Tells us that
an = 7 + (n – 1) x 8
= 7 + 8n – 8
an = 8n – 1 .
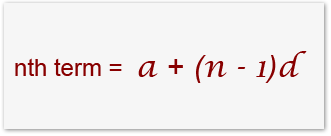
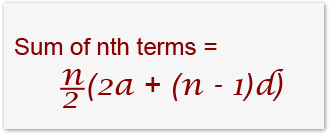
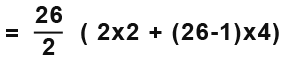
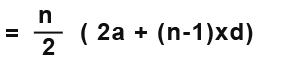
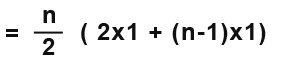



hai ghashh makasakit uLO hindi kuna kaya fulL na taLaga brain kO!! hai sO tired na taLaga huhuhu T_T
Your effort is highly commendable. Thanks for breaking seemingly difficult problems down to simple solutions. However, kindly edit your calculations properly (and check for typographical errors) before posting. E.g. Answer to example 1a is 104 not 10 as mistakenly typed. Thanks. Keep it up
Thanks for the point out.
I have corrected it.