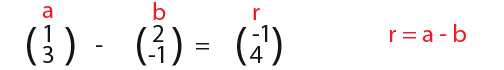Vector Basics
What is a vector?
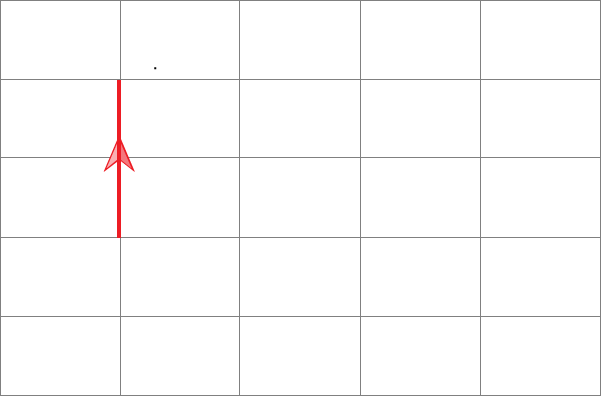
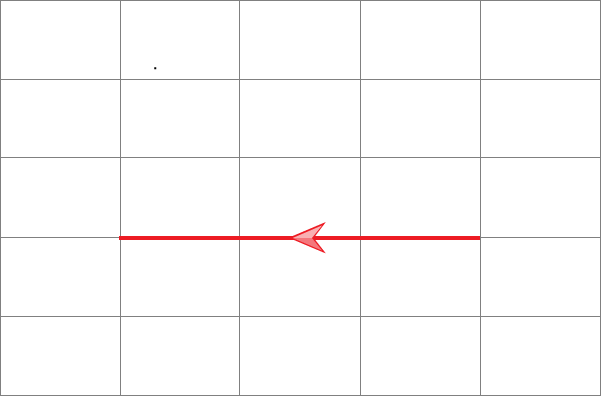
…vectors b on the following to grid shows a large movement to the left. The arrow on the line shows the direction of the movement.
We also use a system called the matrix system to describe vectors.

For example the grid below shows the vector c.
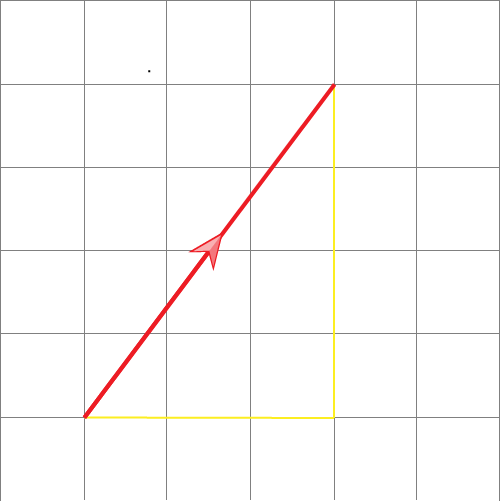
We can see that the vector goes 3 units to the right and 4 units up. That must mean that the vector is;

Below we shall use vector labels for the vectors.

Multiplying vectors

…is shown on the grid below.
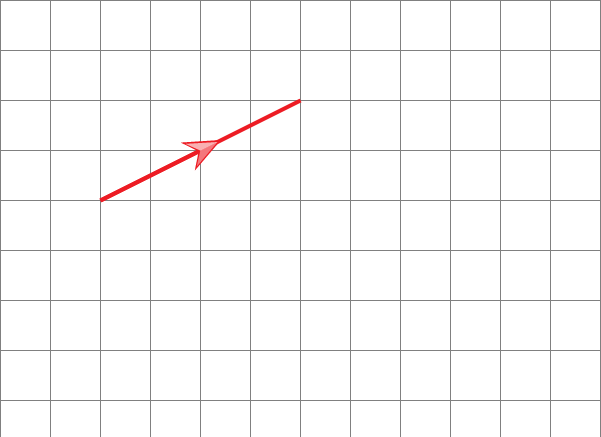
Suppose we wanted to multiply the vector above by 2 so that it becomes 2a. On the grid below is also the 2a vector.
…when
![]()
Suppose we wanted to half it instead of multiplying by 2. On the grid below is also the ½a vector.
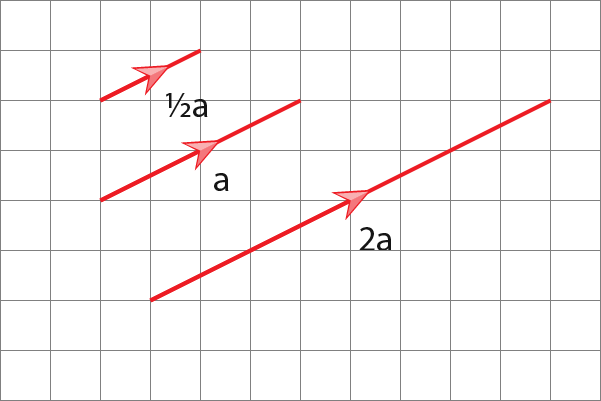
…when;

Suppose we wanted to make the original vector negative. That is to make vector a vector –a. The vector a and vector –a is shown on the graph below.
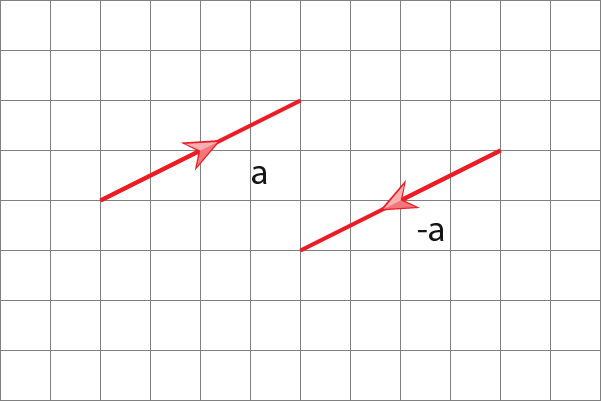
A negative vector goes in the opposite direction of a positive vector. That is when…
![]()
Adding Vectors
![]()
On the grid below is the two vectors a and b.
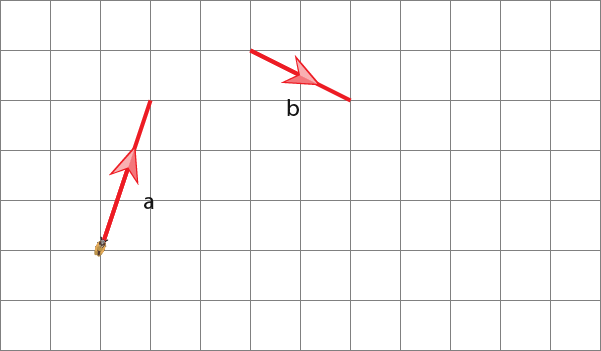
An insect going to move through vectors a+b. The insect moves through vector a first.
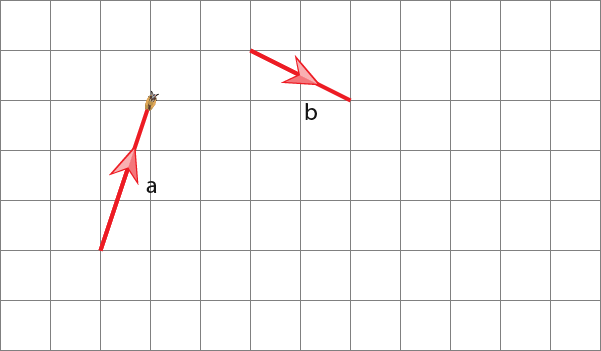
At the endpoint the insect can’t move to the start of b without moving through another vector. So what we do is assume that vector b is at the end of vector a.
![]()
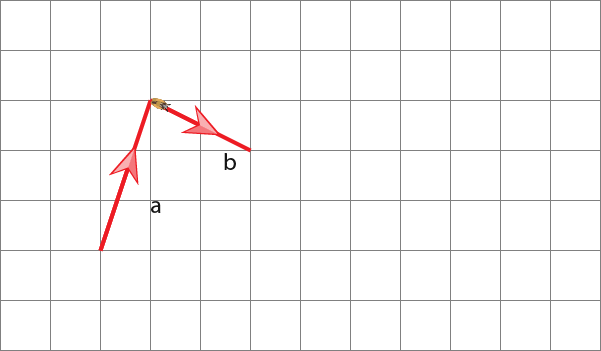
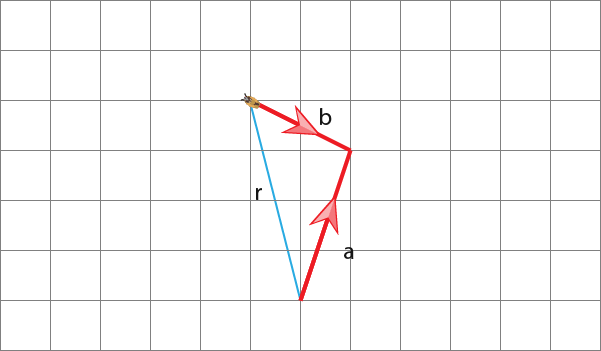
Now the insect can move through vectors a+b as shown above. The insect has travelled a vector of;

But notice below that it could have travelled in the vector blue shown below. This is called the resultant vector.
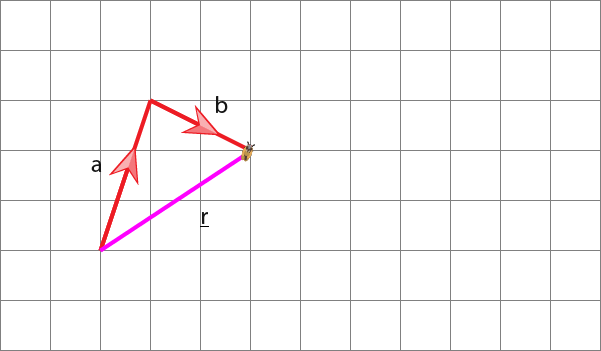
So we have;
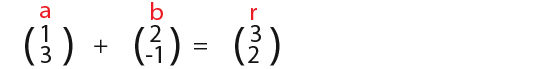
Since adding is possible that must mean that subtracting is possible. Below is the two vectors a and b. This time the insect is going to move through vectors a-b.
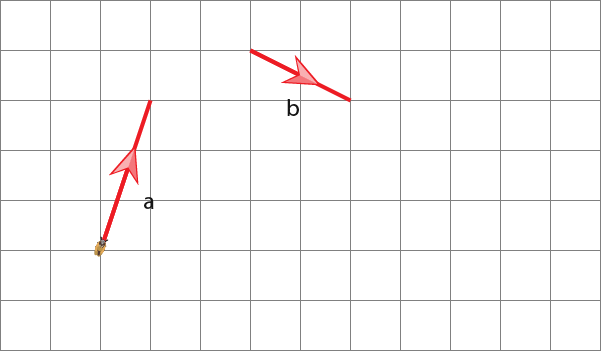
The vector moves through vector a first vector a is;
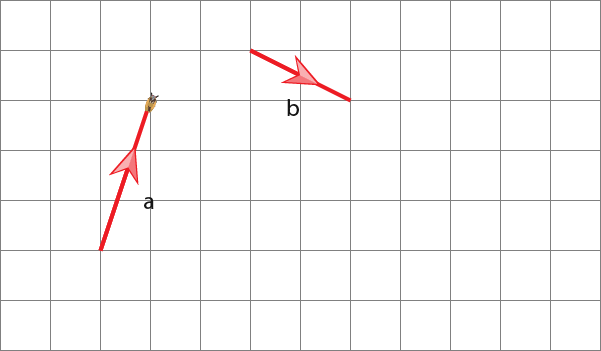
We have a-b, we imagine that this is a+-b. We flip the vector b as shown below such that it moves in the negative direction of b.
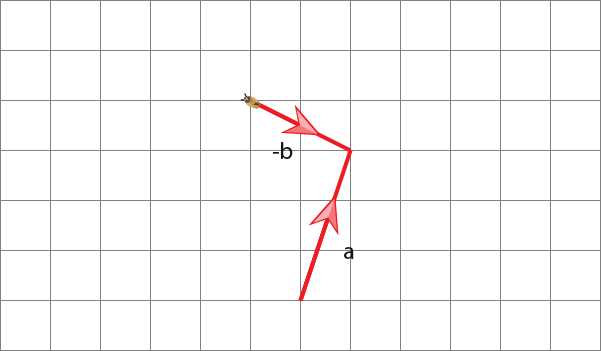
The insect could have travelled in the blue line, This is called the resultant vector.
So we have;