Angles in parallel lines

This chapter explores angles in parallel lines. The objectives of this chapter are; to understand and be able to use alternate, supplementary and corresponding angles in parallel lines.

What are parallel lines?

Parallel lines are lines that are always the same distance apart as they progress. Parallel lines never meet.

We put arrows on the lines to show that they’re going in the same direction and therefore parallel.
Draw two parallel lines and then draw a diagonal (intersecting transversal) that cut through both lines as shown below.

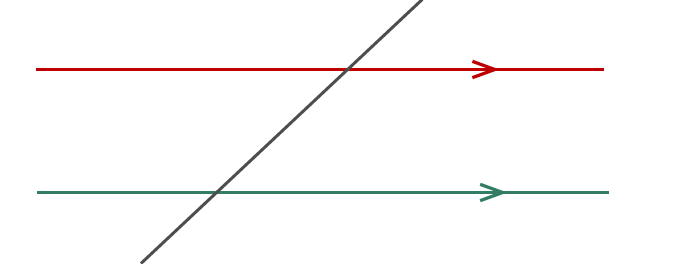
Let’s label any angles that we find where the lines intersect;

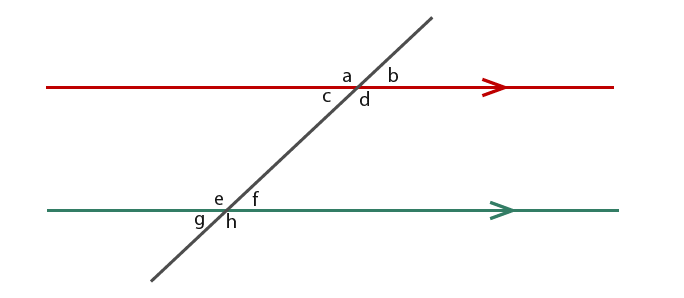
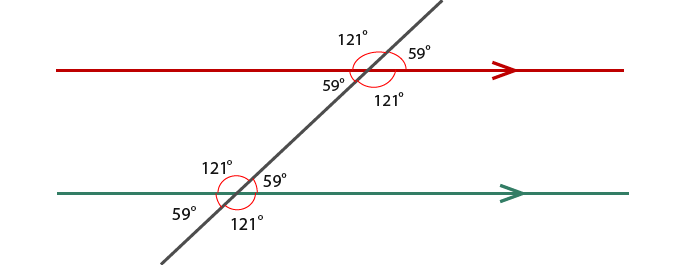
If you use a protractor to find any links between the 8 found angles, you’ll find that there are only two different angles.
Whenever you have a diagonal line cutting parallel lines you create two different angles. One is acute and the other obtuse. An example is shown below;

Alternate Angles

We give angle properties names to help solve problems with angles in parallel lines. For example an “alternate angle”, an alternate angle looks like a Z shape as shown below.

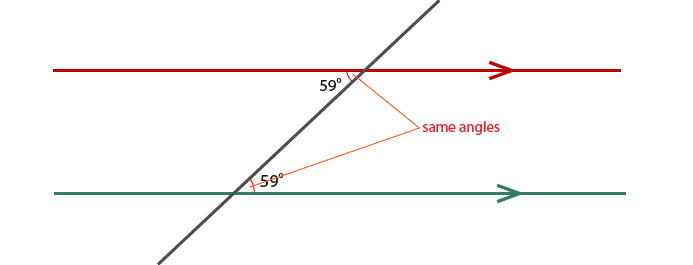
Alternate angles are the same. Alternate angles can also help to find obtuse angles that are the same.

Supplementary Angles

This section explores supplementary angles, supplementary angles form a shape as shown below.

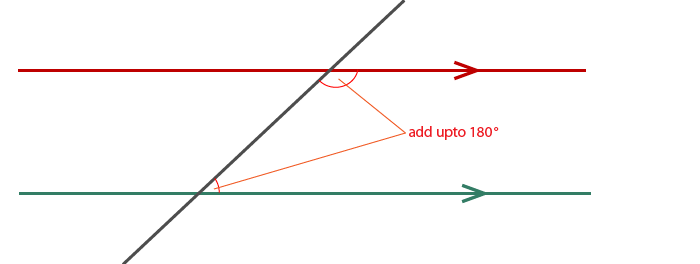
One of the angels above is an acute angle while the other is an obtuse angle. The two angles will always add up to 180°. “Supplementary” means add up to 180°.

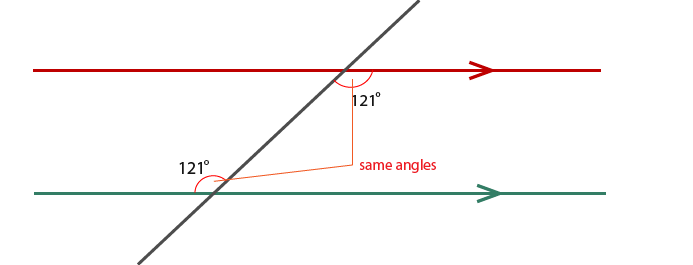
Corresponding Angles

This section explores corresponding angles. Corresponding angles look like an F shape as shown below.

Both angles shown above are obtuse and the two angles are exactly the same.