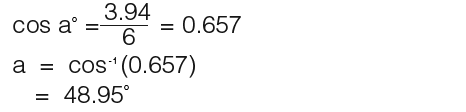Trigonometry Missing Sides
Important notes
In the Trigonometry missing angles we explored the trigonometry formulae and came up with SOHCAHTOA to help in remembering them. The concept explored here is very similar to what we explored in the missing angles chapter. We saw that given the triangle below;
[formulae id=”6″]
Finding missing sides using cosine
This section explores finding missing sides by using the cosine formula;
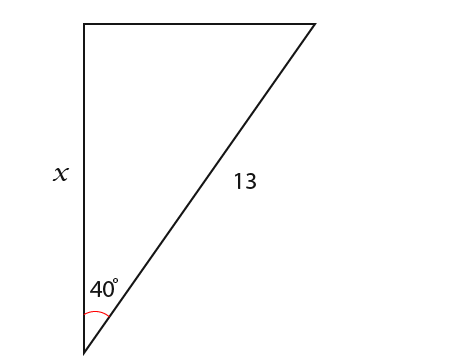

First we identify the sides that are known or available. We have the Adjacent and Hypotenuse x is the adjacent. The Hypotenuse has been given with a value 13.
We must identify what function to use to find the unknown side x. The formulae we have are sine, cosine, or tangent.
In this example we must use the cosine formula because it involves the adjacent and the hypotenuse;

All we have to do is substitute in the known values to find the unknown values as shown below;

We must then rearrange to make x the subject since it is the value that we are after.
![]()
Now we need to work out the value of 13cos(40°) on the calculator and round off to 2d.p, the answer would be;
![]()
Finding missing sides using sine
In this section we shall explore how to find missing sides of triangles by using the sine formula.
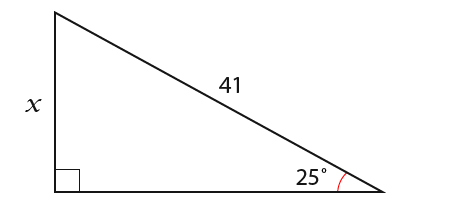

First we identify the known sides. We know the Opposite and Hypotenuse; x is opposite while 41 is the hypotenuse. Next we need to identify the function to use; whether sine, cosine, or tangent.
Above we can see that we need to use the sine function. The formula that we need to use is shown below.

Then we substituted in the values in the formula.
![]()
…next we rearrange to get x on its own since it is the value that we’re trying to find;
![]()
Next we work out 41sin25° calculator and round off to 2 decimal places.
![]()
Finding missing sides using tangent
This section explores how to find missing sides using tangent. The triangle shown below should help in this practice.
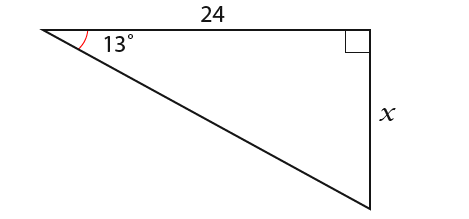


First we need to identify the known or available sides. We know the Opposite and Adjacent; x is opposite while 24 is the adjacent. Next we need to identify the function to use;
The function to use is the tangent formula as we can see above the function states that;

Next we substitute in the known values as shown below;

…then we rearrange to get x on its own since it is the value we’re trying to find;
![]()
Next we work out 24tan13° on the calculator and round off to 2 decimal places.
![]()
x on the bottom of the equation
You’ll find some difficult when x is on the bottom of the equation. The triangle below should help to explore the problem;
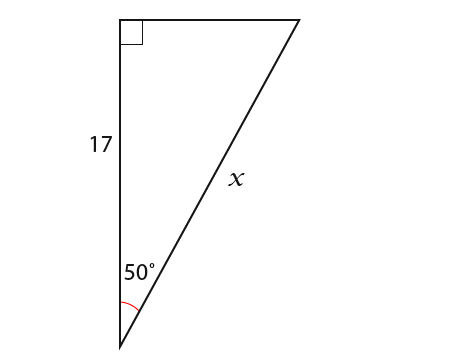
First we identify the knowns sides. In the triangle above we know the Adjacent and Hypotenuse. 17 is adjacent and x is the hypotenuse, looking at;
…we can see that the function to use is cosine. Therefore;

We simply substitute in the known values;
![]()
In this instance the x is at the bottom of the equation this makes it much harder to rearrange to make x the subject unless you have encountered this form of rearranging before. First multiply both sides by x or cross multiply as shown below.
![]()
…that gives;
…next we divide both sides by cos50° to result in;
![]()
This results to the following answer to 2 decimal places.
![]()
Exam question
In this section we shall look at a previous exam question;
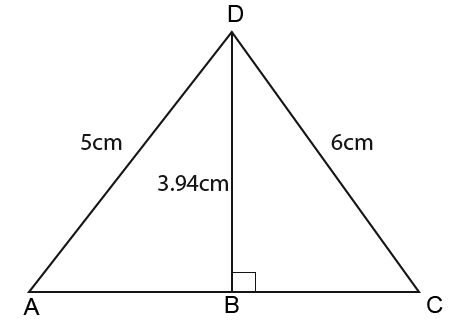
- Calculate the length x
- Calculate the angle CDB

-
Let angle CDB = a