Lines and Quadrilaterals

This chapter explores lines and quadrilaterals. The objectives for this chapter are; Imagining and describing 2D shapes, Parallel and perpendicular lines, properties of rectangles and squares and properties of common quadrilaterals. No prior knowledge is required for this chapter.

Parallel and perpendicular lines

This section explores parallel and perpendicular lines. Lines that travel in the same direction can never met. We say that the lines are parallel. The lines below are parallel.

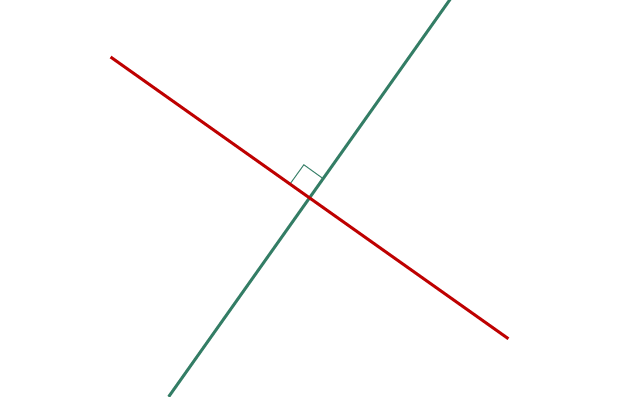
We indicate/show parallel lines with arrows as shown above. When lines meet at right angles such as that shown below…

…we say they are perpendicular. We show lines are perpendicular line below.

Quadrilaterals

The shape of quadrilateral is shown below. It is a shape with 4 straight edges.

There are 6 special quadrilaterals.

Square

A square has opposite sides parallel and all angles are 90° throughout the square. All the sides are equal. A square is also a special rectangle with all sides equal.

Parallelogram

A parallelogram has all opposite sides parallel and opposite sides equal.

Rectangle

A rectangle has opposite sides parallel. All angles are 90° and opposite sides equal.

Rhombus

The rhombus has all opposite sides parallel and all 4 sides are equal. A rhombus is a special parallelogram with all sides equal.

Trapezium

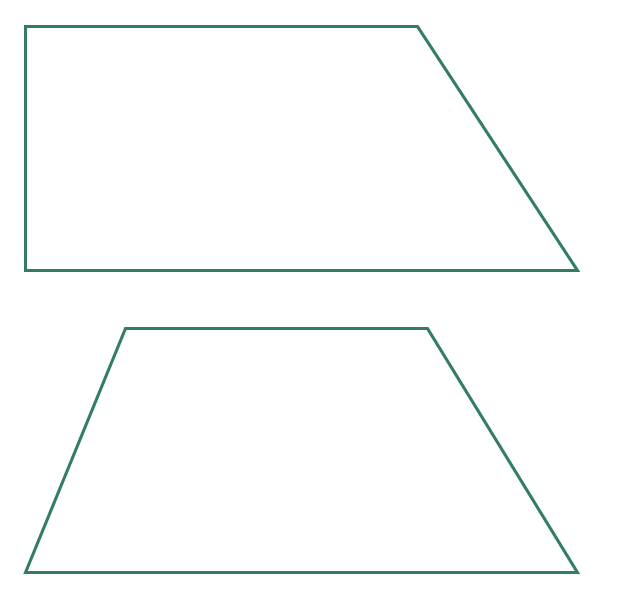
The trapezium has one pair of opposite sides which are parallel.

Kite

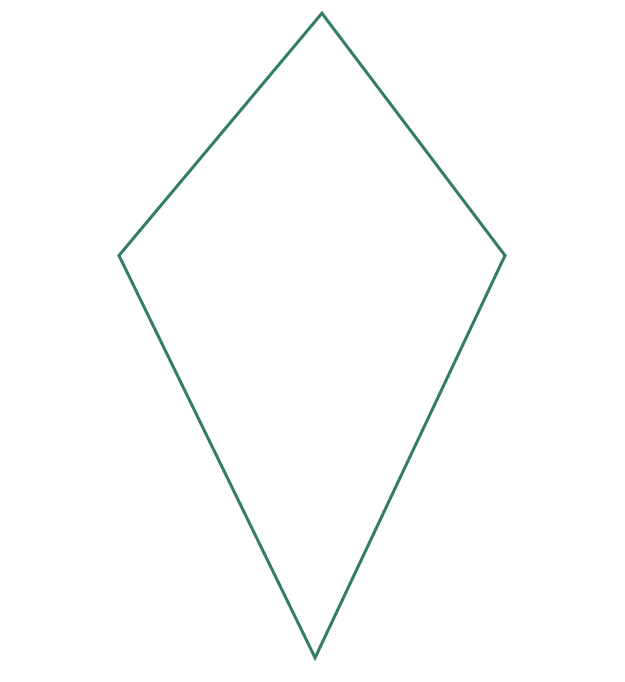
A kite has two pairs of equal sides. The equal sides are adjacent to each other rather than opposyite.

Diagonals

The shape below is a rectangle.

The diagonals are now shown in the rectangle.

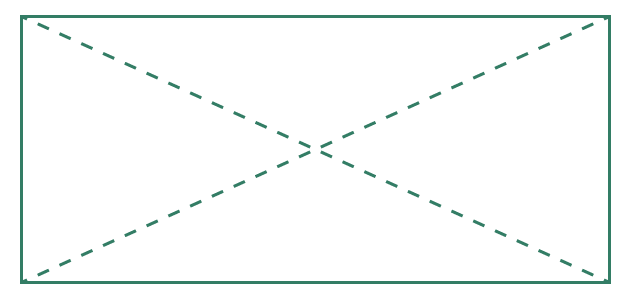
The diagonals are equal in length and they cut each other in half. Suppose we turned the rectangles above into a square to observe the diagonals.

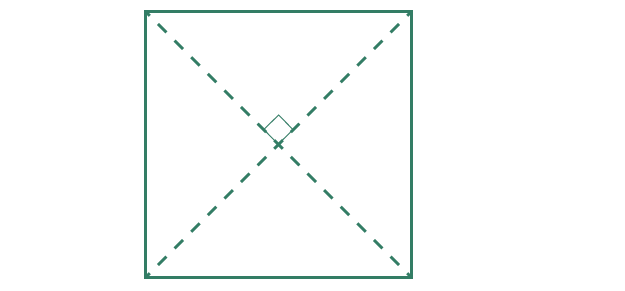
If you use a protractor you’ll notice that the diagonals of a square cross each other at 90°.
The shape below is a parallelogram and with its diagonals.

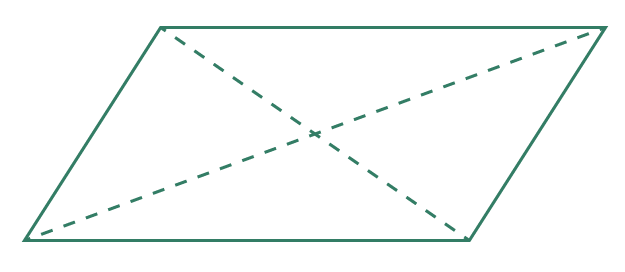
If you use a ruler to measure the length of the diagonals you’ll notice that they’re not equal.
If we turn the parallelogram into a rhombus as shown below.

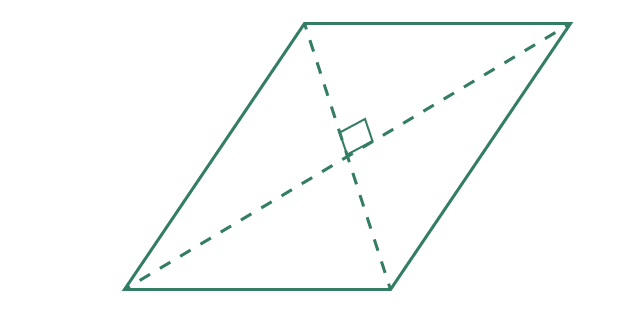
…you’ll notice that the lengths of the diagonals are not equal as well, however they do cross at 90° if you check with a protractor.

Kite diagonals

Another quadrilateral which has diagonals that cross at 90° is the kite.

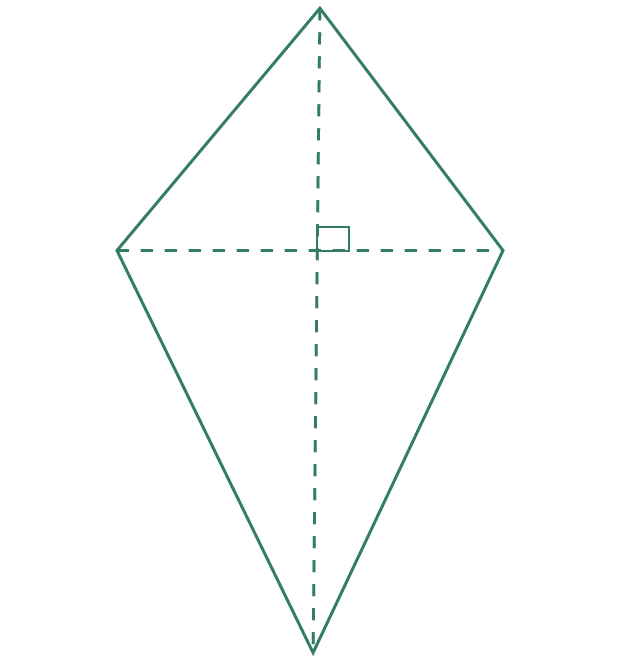
Only one of the diagonals is cut in half.