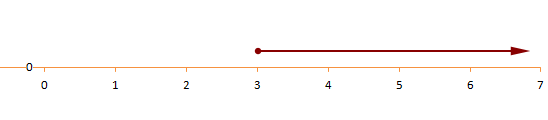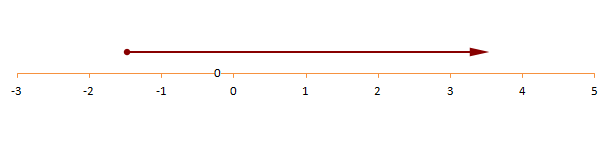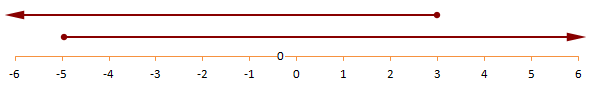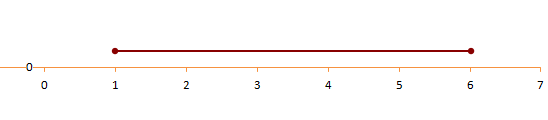Linear Inequalities
Equations and inequalities connection
You must already know how to solve linear equations for example below is an equation to solve naturally.
First we expand the equation as shown below.
Arrange x terms on one side as shown below.
Now we can simplify as shown below
We divide both sides by 7 and the result becomes.
We can use the same principle used above to solve the following inequality.
First we expand as shown below.
Rearrange
…and simplify…
…then divide both sides by 7 to simplify again. We get that;
We can also indicate this on a number line to get a better visual as shown below.
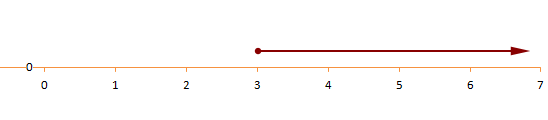
Negative coefficient of x
And then move the integer to the other side as shown below.
The result becomes;
We divide both sides by 4 and the result becomes;
or
The other alternative is not moving the term with x and move 16 instead.
We divide both sides by -4 and the result becomes;
The solution can also be shown on a number line as shown below.
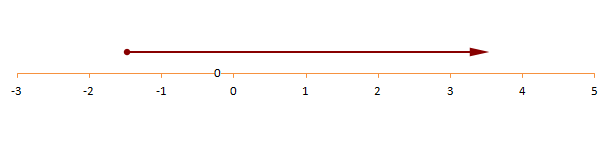
You must have noticed that when you divide or multiply by a negative, the inequality changes direction.
Double-ended inequalities
Now we can solve each part separately as have been done below.
Now we can put the solution back together to result.
The solution has been shown on the number line below.
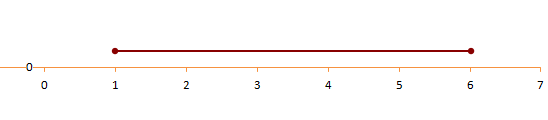
Solving inequalities in a pair
You could also work out where two solutions overlap. For example suppose we had to find the values which satisfy both inequalities shown below.
First we solve the first inequalities.
Then we solve the second inequality
We have;
We can look at both solutions on a number line.
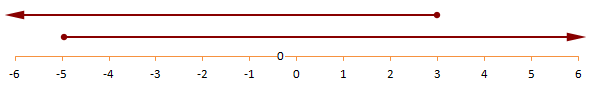
The solutions as we can see above overlap between -4 and 3.
Exam question
First we find an expression for the perimeter.
The perimeter is greater than 28cm and less than 36cm.
The inequality contains two parts so we solve each part separately.
The range of values x can take are;
We know that AB is an integer so we look for whole numbers in the range that is;
The length of AB is either 11cm or 12cm.
13 has not been included in the final answer.
