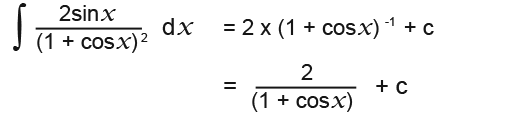Integrating fractions

This chapter explores integrating fractions. It covers recognising integrals of the form;

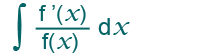
…and integrating fractions using the chain rule backwards. Before attempting this chapter you must have prior knowledge of integrating simple fractions by inspection using the chain rule.

Remainder

In the previous chapters we discovered that;

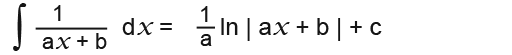
…we also discovered that to integrate simple fractions we need the natural log, that is;

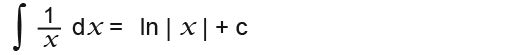
Also remember that if;

…then…

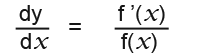
…which leads to the conclusion that;

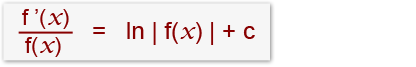
For example…

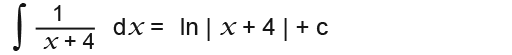
…we know that the differential of x+4 is 1. We can form a much simplified general rule which states that;

…we can extend further and write;

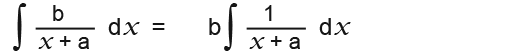
…from above we can form a general conclusion that;

Do you remember how to integrate the following;

We could guess that the result will be;

…we assume that the above answer is true and then try to differential it;

…that means we need;

So that when differentiated we get;

So we can conclude that;

…while…

In general

Integrating using inspection

There are certain tips to remember when integrating fractions. For example is the top line of the fraction is the differential of the bottom then the answer is simply “ln |f(x)|” that is;

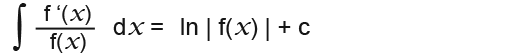
Example

Here is an example. Note from the following example that 5x + 3 differentiates to 5.

Let’s assume the result is;

Then when we differentiate we get;

As we have seen the top line of the integral is exactly the differential of the bottom. So we can conclude that;

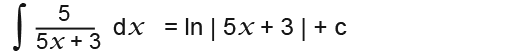
The rule also applies for fractions other than linear ones, for example;

Above we can see that the top is almost the differential of the bottom we can guess that the answer is;

We can differentiate it to check whether it is correct.

Above we have an extra factor of 2 which we have to cancel out as shown below.

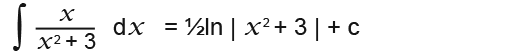
The following are some harder examples of fractions in the form of;

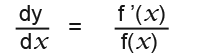
Example

Find the following integral

Above we can see that the top is nearly the differential of the bottom that is;

Let’s try;

So now when differentiated we get;

We have to adjust the factor of 4.

So the final integral becomes;

Example

Find the following integral

Again here the top is almost the differential of the bottom that is;

Let’s try;

…trying to differentiate…

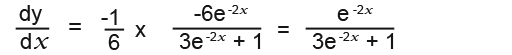
We can conclude that the final integral is;

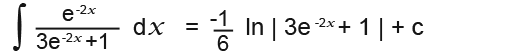
Example

Find the following integral

First let’s convert the integral into a fraction as shown below;

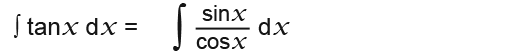
Now we can see that the top is almost the differential of the bottom because;

We can guess that the answer is;

Now we need to check it by differentiating it;

So the integral must be;

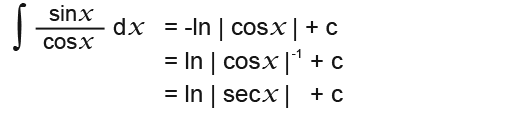
We conclude that;

Some functions are easy to integrate but don’t involve logs, for example;

Here the top is not the differential of the bottom because of the power of 2. To make the entire process easier we rewrite it as;

Let’s guess a function which differentiates to give (2x + 3)^-2. Let’s start by adding 1 to the power to get;

Now let us try to differentiate it by using the chain rule;

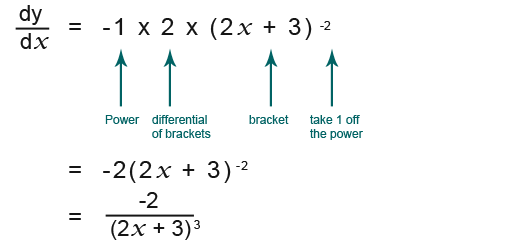
…and…

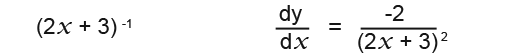
…we have…

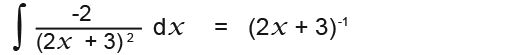
Remember we were asked for the integral of;

We must take into account of the -2 factor;

So we can conclude that;

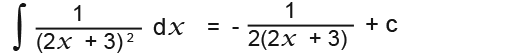
Below is another example that we could try. “Find the following integral”

First we simplify it to make the process easier;

Now let us guess that the answer is;

…we can check it by differentiating it;

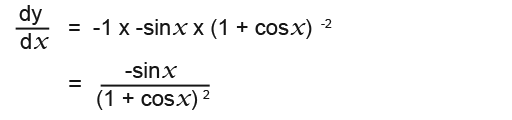
So the integral must be;