Integration by Parts – Twice

This chapter explores integration by parts twice. The chapter covers using the method of integration by parts twice to integrate much more complex functions, and using standard trigonometric integrals in integration by parts. Before attempting this chapter you must have prior knowledge of integration by parts and standard trigonometric integral results.

Integrating by parts

You should already be aware of basic methods of integrating by parts. You must know that the formula for integration by parts is;

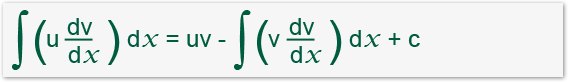
Sometimes the method requires to integrate by parts twice for example finding the following;

…we have to compare it with integration by parts formula;

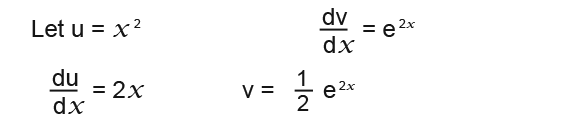
Now we can substitute in the expression we get;

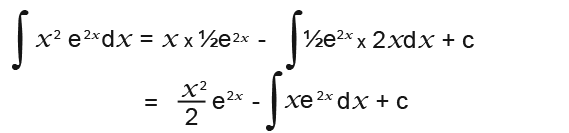
..we need to integrate by parts again
[IMAGE]
Let;
[IMAGE]
…to find v above we integrate dv/dx
Now we can substitute in again;
[IMAGE]
The final integral becomes;
[IMAGE]
…we can simplify it further by taking out a common factor.
[IMAGE]
Below are more examples.

Example

Find;
[IMAGE]
Let;
[IMAGE]
Now we can substitute in the values;
[IMAGE]
…we integrate by parts again. Let;
[IMAGE]
The integral becomes;
[IMAGE]
[IMAGE]

Example

Find;
[IMAGE]
Let;
[IMAGE]
…we substitute in the values to get;
[IMAGE]
…we integrate by parts again. Let;
[IMAGE]
The integral becomes;
[IMAGE]
[IMAGE]
[IMAGE]

Harder integration by parts examples

The following are harder integrals. It might be useful to have memory of some standard trigonometric integrals.

Example

Find;
[IMAGE]
First we let;
[IMAGE]
Remember that;
[IMAGE]
The integral becomes;
[IMAGE]
…remember also that the following is a standard integral and appears in the integral above;
[IMAGE]

Example

Find
[IMAGE]
Let;
[IMAGE]
[IMAGE]
…remember sec²x is a standard integral.

Example

Find;
[IMAGE]
This integral is quite tricky, we have to find which part to make u. Neither e^x nor cosx are simplified when differentiated. Let’s try;
[IMAGE]
…we substitute in to get;
[IMAGE]
…we integrate by parts again. Let;
[IMAGE]
…we substitute in the values;
[IMAGE]
You might have noticed that two parts highlighted above are the same as the original integral. Let;
[IMAGE]
So now we have;
[IMAGE]
[IMAGE]
Therefore…
[IMAGE]
[IMAGE]