Equation of a line 2
This is the second part for the equation of a line chapter. This covers understanding that a line can be described using an equation, understanding how gradient and intercept affect a line, sketching lines using m and c and rearranging equations to find m and c. Before attempting this chapter you must have prior knowledge of rearranging equations.
About line equation
Here we shall explore what a line equation is.
A line equation is a rule. It can be used to identify a line coordinates. The line may be straight or curved. We shall be looking at rules for straight lines. Below is a rule example;
![]()
The rule simply states that whenever you add the x and y coordinates you always get 100.
The rule line looks like the following.
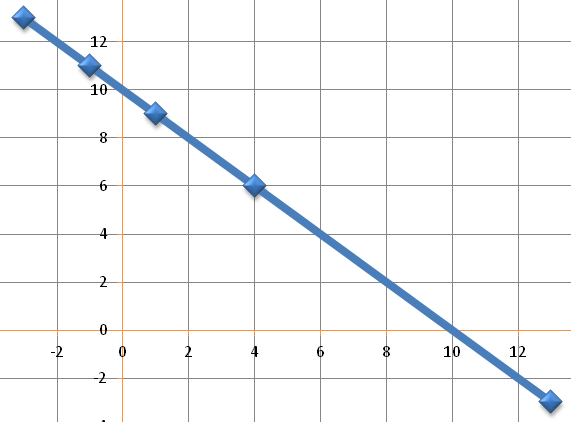
Below are some of the coordinates which lie on the line.
![]()
You can use the rule to check whether they obeynit.
Below is a different rule;
![]()
The rule simply means if you multiply the x coordinate by 4 and add the y coordinate you always get 9. The line looks like the following.
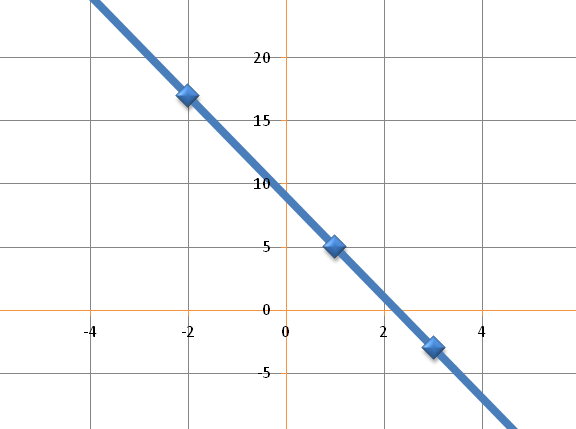
Below are some of the coordinates that lie on the line;
![]()
Exploring m and c
The general equation of a line is;
![]()
…where m and c can be any values.
Gradient
The mathematical term for steepness is gradient. The equation y=mx + c, m affects the steepness of the line.
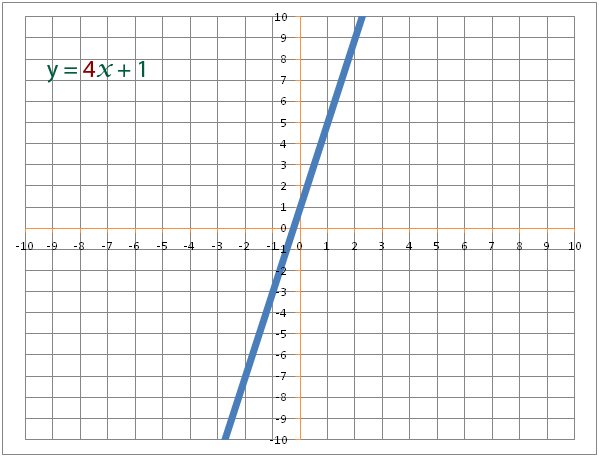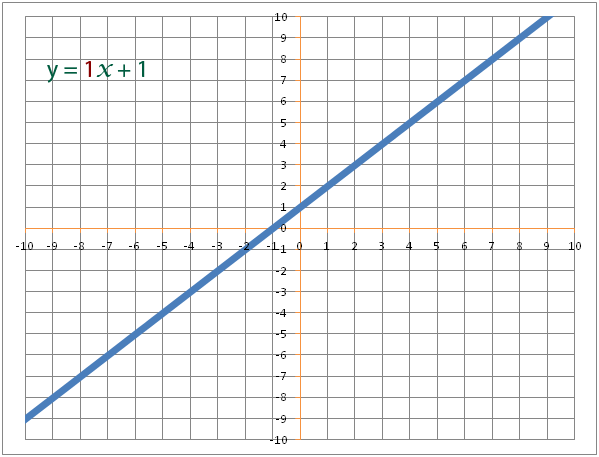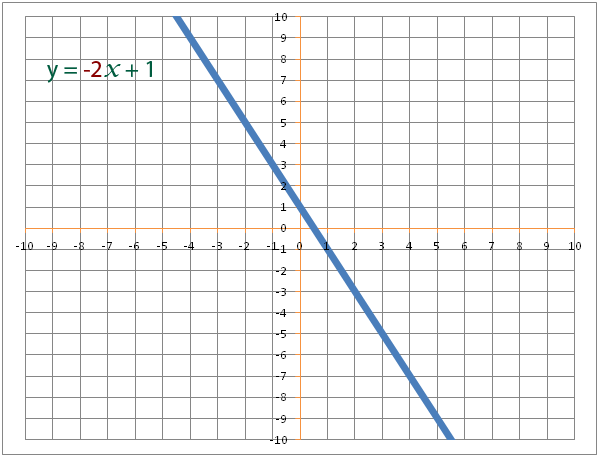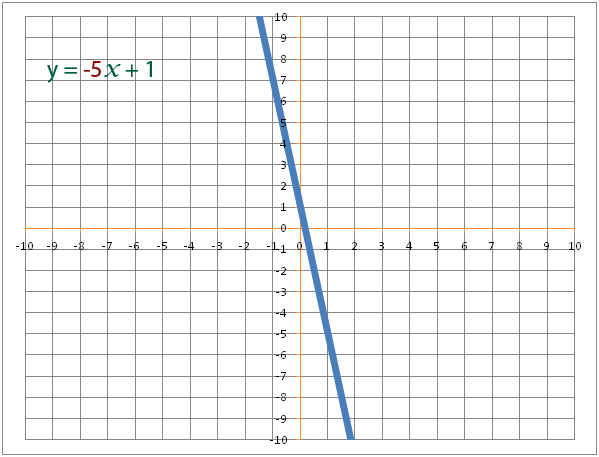
The gradient is the number of x’s in the equation. The equation y=7x -3 has a gradient of 7.
The gradient is the measurement of how far up a line travels for every unit going across. For example let us look at the line with the equation y = x + 2. The line travels up 1 unit for every unit across as shown below.
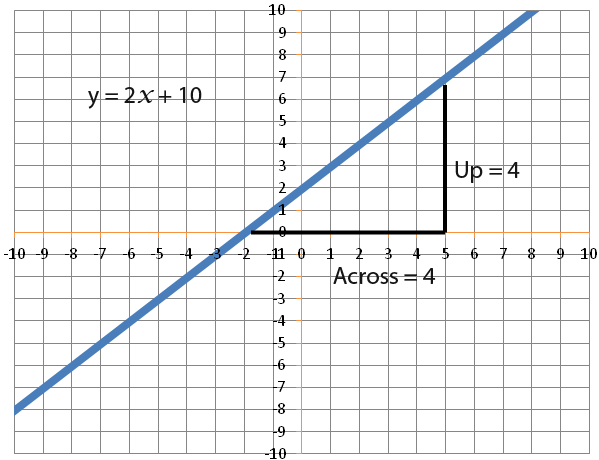
The line above has a gradient of one. Now let us look at another line with the following equation.
![]()
The line travels up 2 units for every unit across.
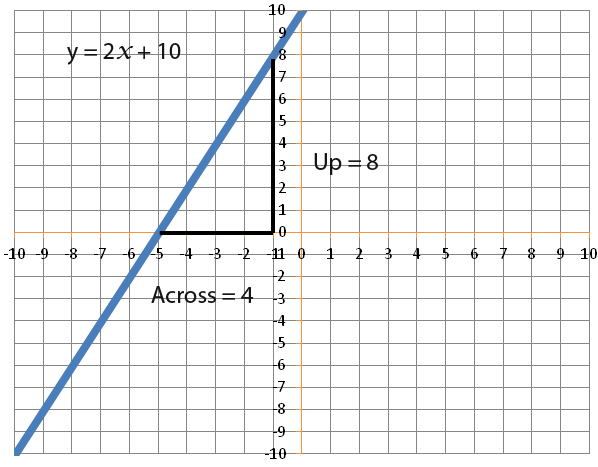
The line above has a gradient of 2.
Let us look at another line with the following.
![]()
The line travels up 1 unit and across 2 units. So it must go up 1/2 for every unit across, therefore having a gradient of 1/2. The line is shown below.
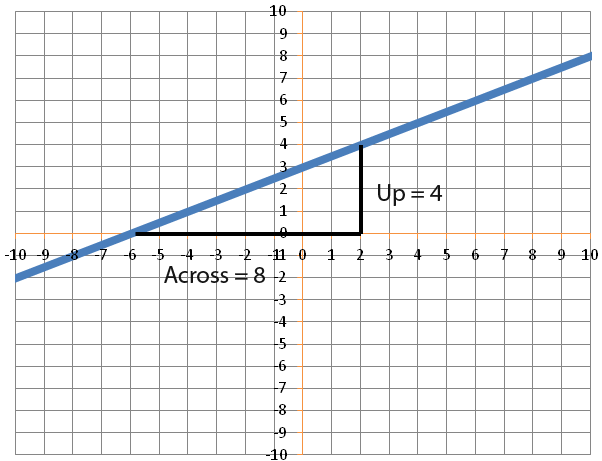
Intercept
The graph my also change its height. The value of c indicates where the line cuts the y axis. This is known as the intercept or the y-intercept.
![]()
Quick Summary
Here is a quick summary.
The equation of a straight line is given in the form of;
[IMAGE]
…where m is the gradient.
To work out the gradient, you pick any two points on line such as;

Then use the following formula.

Rememer c is the intercept. This is where the line cuts the y axis.
Sketching a line by rearranging
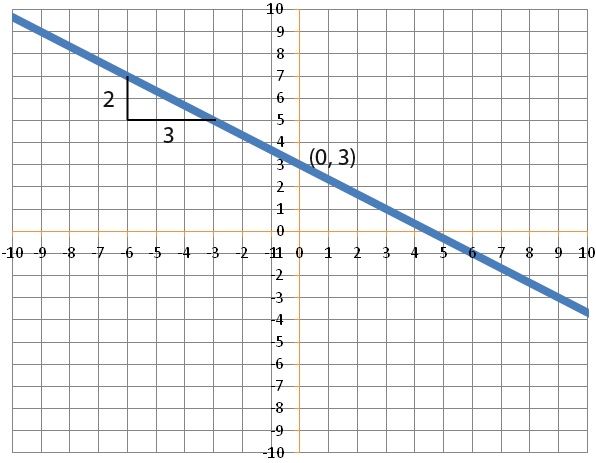
In this section we shall explore sketching a line. Suppose we wanted to sketch the following line.

To simplify we rearrange the equation into the form y=mx + c to find the gradient and intercept.
![]()
Now we know that;

The line crosses the y axis at (0, 3). The line looks like the following.
Parallel lines
You may come across situations where you have to test if lines are parallel.
Two or more lines are parallel when their gradient (m) is the same.
Suppose we had to find out whether the following two lines are parallel.

First let us rearrange the first equation.

Now we know the gradient for the first equation is;
![]()
Now let us rearrange the second equation.

We now know the gradient for the second line is;
![]()
We can conclude that since that the gradients are the same, so the lines must be parallel.
