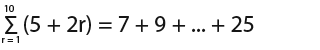Sequences and series notes

Below are some sequences and series notes. They should help when working with sequences and series.

1. A series of numbers following a set rule is called a sequence.
   
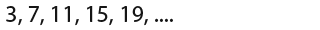
   …is an example of a sequence
2. Each number in a sequence is called a term.
3. The nth term of a sequence is sometimes called the general term.
4. A sequence can be expressed as a formula for the nth term, for example;
   
   …produces the sequence;
   
   …by replacing n with 1,2,3,4 etc in 4n + 1.
5. A sequence can be expressed by a recurrence relationship for example the same sequence 5,9,12,17,… can be formed from;
   
   …in all cases U must be given.
6. A recurrence relationship of the form;
   
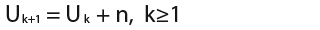
   …is called an arithmetic sequence.
7. All arithmetic sequences can be put in the form.
   
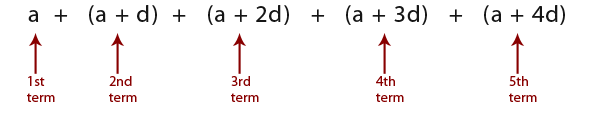
8. The nth term of an arithmetic series is a + (n-1)d, where a is the first term and d is the common difference.
9. The formula for the sum of an arithmetic series is;
   
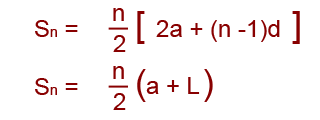
   …where a is the first term, d is the common difference, n is the number of terms and L is the last term in the series.
10. You can use ∑ to signify ‘sum of’. You can use ∑ to write series in a more concise way, for example;