Stationary Points

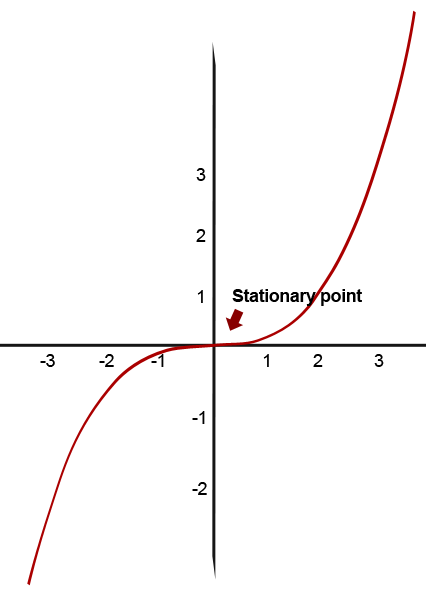
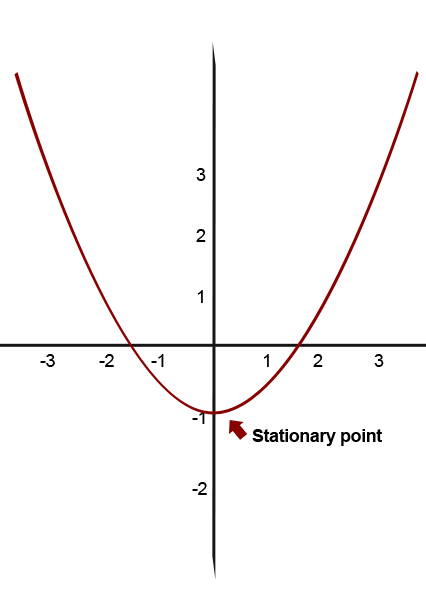
A stationary or turning points on a graph, is the point where the gradient is equal to zero. It is often useful to find and understand the stationary points on graphs especially in engineering. The following illustration shows a graph with a stationary point.

Graph showing stationay point

Graph showing stationay point

The pointer in the illustration shows a turning point. It is the flat area on the graph which is referred to as a stationary point.

You must know that a straight line in the x-axis has a gradient of zero. This makes perfect sense with stationary points having a gradient of zero.

For example

Find the stationary point on the function of y = x² – 4x + 4

This is a quadratic graph note by the x². We are asked to find the x and y coordinate of the stationary point. To find the stationary point we would have to differentiate the function because we know that the stationary point is found where the gradient is equal to zero.

f'(x) = 2x – 4
The stationary point is at where f'(x) = 0 so;

2x – 4 = 0
2x = 4
x = 4/2
x = 2

Now we know the x coordinate of the stationary point, we can use the original function to find the y coordinate.

y = x² – 3x + 2
y = 22 – 3 x 2 + 2
y = 0

The stationary point is at (2, 0)

Determining the nature of the stationary points

You might be asked to determine the nature of the stationary points.