Expressing acosθ + bsinθ in terms of cosine and sine functions

This article is a continuation from the previous trigonometry article. This article covers how to write expressions of the form acosθ + bsinθ , where a and b are constants, as a sine or cosine function only.
Using the addition formulae, we can shows that all expressions of the form acosθ + bsinθ can be expressed in either;

You must be aware that the graph of y=af(x – α) is the graph of y=f(x) stretched vertically by a factor of a and translated by α. We can use the ‘R formula’ to solve equations of the form acosθ + bsinθ = c, where a, b, and c are constants but if c=0, the equation reduces to the form tanθ = k. Expressions of the form asinθ + bcosθ can be rewritten in terms of sine and cosine using the following rules when a and b are positive.

…with R>0 and 0<α<90° ...where Rcosα = a and Rsinα = b and R =√(a² + b²) Below we shall explore through some examples;

Example

In this example we shall show that 3sinx + 4cosx can be expressed in the form Rsin(x + α), where R>0, 0<α<90°. We shall also note down the values of R and α Note also here that we know that;
If we multiply the expression through by R we get the following expression;

…since we’re trying to write 3sinx + 4cosx into Rsin(x + α) we let;

Note here as well that for the above expression to be true all values of x, the coefficients of sinx and cosx on both sides have to be equal therefore…

…we need to find R and α.
Let us start by finding α. We know that sinα divide by cosα is tanα, therefore we could;

…so since sinα over cosα is tanα we get;

Next we shall find R. To do that we shall square Rcosα and Rsinα and add them together then we shall find R² so we have,

…factorise the left hand side to get;

Remember cos²α + sin²α is equal to 1, that must mean that;

We have managed to find R and α to rewrite 3sinx + 4cosx as Rsin(x + α)so we have;

Note here also you could rewrite;

…by setting…

…and then solve to find R and α.

Example

Here is another example, In this example we shall express sinx -√3cosx in the form Rsin(x – α) …we shall also sketch the graph of sinx – √3cosx. First we want;

…and we know that this gives;

Note that for RHS we have simply expanded sin(x-α) and multiplied by R. Using the expression above we find that;

…we have compared the coefficients of sinx and cosx on both sides of the expression. We need to find α first and we know that sinα/cosα = tanα so we divide Rsinα by Rcosα;

The Rs cancel each other out, so we find that;

…we do the same to find R as we did above;

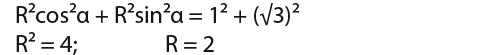
…we can conclude that;

The graph is simply a sketch and a translation. To sketch 2sin(x – π/3), we translate y=sinx by π/3 to the right and then stretch it by a scale factor of 2 in the y-direction as shown below;
[visualizer id=”5549″]

Example

In this example we will express 2cosθ + 5sinθ in the form Rcos (θ – α) and then we shall solve the expression 2cosθ + 5sinθ = 3 for 0 < θ < 360° We need to express;
…we know α should be between 0 and 90° and R should be greater than 0 and we know that;

…so we have;

We shall need to compare the coefficients of sinx and cosx on both sides of the expression, so we have;

Another method we could use to find R is by making R the subject in the expressions above. Then draw the triangle for example Rsinα = 5;

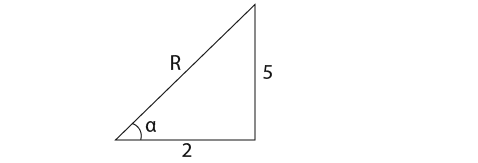
…so we get;

…and…

…since we have worked out R and α, we find that;

Now we need to solve the equation 2cosθ + 5sinθ = 3. The solutions will be the same for √29cos(θ – 68.2°) = 3 as we have found out above; 2cosθ + 5sinθ = √29cos(θ – 68.2°). We simplify both sides by √29 so we have;

Using the calculator to find;

…so now we’re trying to find θ – 68.2°