Geometric progression/sequences
A geometric series or progression is a series where each term is found by multiplying the previous term before it by a constant number. This constant number is called the common ratio (r).
Here is a geometric series; 3+6+12+24+48+…
The common ration of this geometric series is a 2.
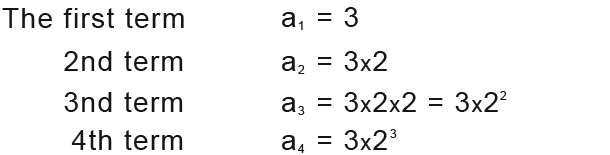
There is a pattern as you probably might have realised by now. We can find the 10th since we’ve realised the pattern.
10th term a10 = 3×29
The formula for the nth term of the above geometric series is;
an = 5 x 2n-1
So for a general geometric series with first term a and a common ratio r;
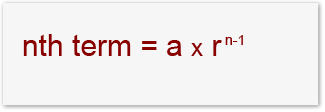
Here is another example of geometric series; 1+3+9+27+81+…
This is a geometric series with a=1 and r=3. What is we wanted to find the sum of this series up to 100 terms.
The sum up to 2 terms is;
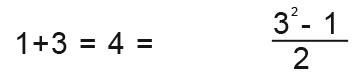
Up to 3 terms;
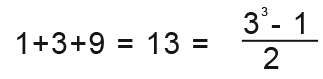
Up to 4 terms;
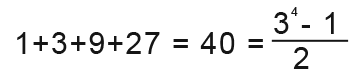
Do you note something here? All the terms are;
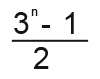
We can conclude that; Provided that a=1 the sum of a geometric series with a common ratio r is;
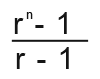
Take for example; 1+3+7+10+…
a=1 and r=3, so the sum of n terms for this geometric series is given by;
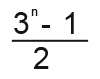
You have to note that this formula will only work when the first term in the series is one or a=1.
The following is the general formulas for working out the nth term and the sum of the nth terms even when a=1.

Example1
Find the 5th term and the value of; 5+15+45+135+… to 10 terms.

Example2
Find the 4th term and the value of; 5+20+80+320+… up to 10 terms.
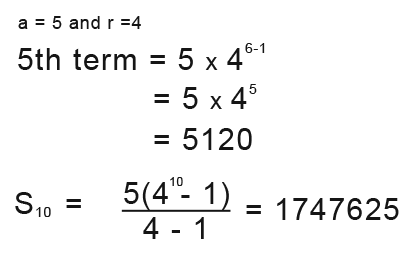
Sum of nth terms when the common ratio (r) is small
The able formulas will not work when the common ratio (r) is between -1 and 1 (really small). For example here is a series where the common ratio is small; 5+2.5+1.25+0.625+… r=0.5.
Observe as we work out the sum of the nth terms;
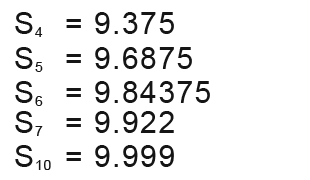
You must have realised that the sum is getting closer and closer to 10. Also as the series continues the terms get much smaller and smaller. After the 100 terms the term we add on is really tiny that we’re aren’t really adding on anything.
Here is why the series get closer and closer to 10.
This is our sum formula;
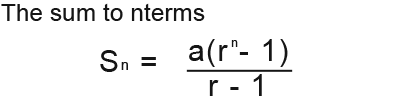
For our geometric series above a=5 and r=0.5
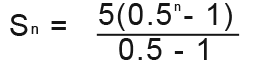
In the above expression as n gets close to infinity (¥; this is the infinity symbol) the 0.5n gets very very tiny.
![]()
This means Sn gets very close to 10;
![]()
For this we say that;

Geometric series only converge if rlies between -1 and 1. So if the geometric series converges then the formula for the sum to infinity reduces to;
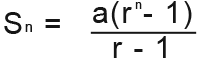
In general;
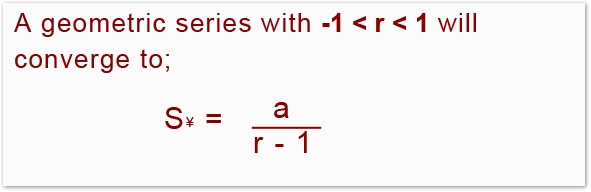
Example
Find the sum of infinity of the geometric series; 3+0.6+0.12+… for this geometric series; a=3 and r=0.2
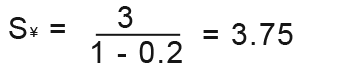
Example 2
Find the sum to infinity of the series; 0.2+0.1+0.05+… for this geometric series; a=0.2 and r=0.5
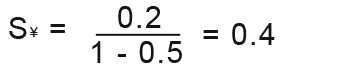
Example4
Find the sum to infinity of the geometric series; 0.5+0.1+0.02+… for this geometric series; a=0.5 and r=0.2
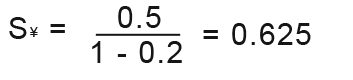
Example5
Find the sum to infinity of the geometric series; 0.5+0.05+0.005+… for this geometric series; a=0.5 and r=0.1.
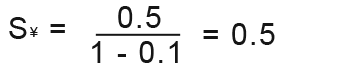

1 Response
[…] can read more on Geometric progression/sequences here. VN:F [1.9.6_1107]please wait…Rating: 0.0/10 (0 votes cast)VN:F [1.9.6_1107]Rating: 0 (from 0 […]