Before attempting this maths learning it might be a good idea to go through the lesson of finding the area below the curve along the x-axis, because I won’t cover the basics and the details here.

You must know that to find the area between the curve and the axis we integrate as below.


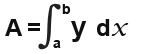
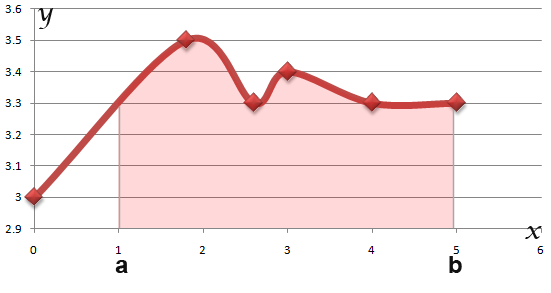
where a and b are the x values as shown on the graph diagram.

Well finding the area between the curve and the y-axis is very similar supposing you know how to find the area between the curve and the y-axis.

We simply find the x in the y function by making x the subject and then integral becomes;

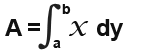
where a and b are the y-values, it is very important that recognise that it is along the y-axis instead of x.

Example 1

Find the area of the shaded region y = √x + 1 between y=2 and y=3

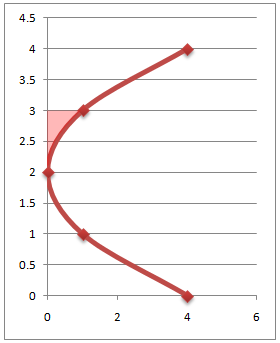
First we would need to find the x equation from our function by making it the subject as follows.

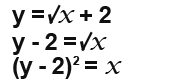
Now we need to integrate x between the given y bounds.

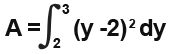
We integrate by inspection

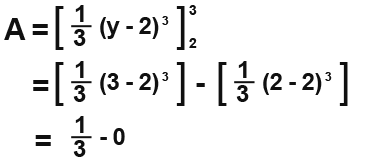
Example 2

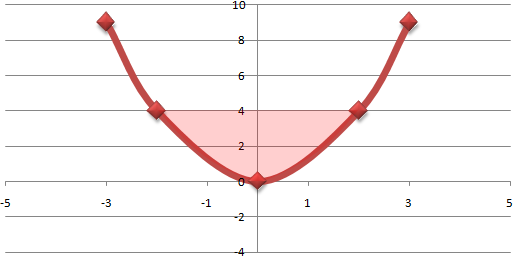
Find the area between the curve and the y-axis between y=0 and y=4 for y=x2

The problem has been shown on the graph below.

We know the formula for the area is:

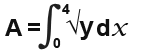
We first had to to find the x equation from the y function. You have to be careful here the above expression will only give us the area between the curve and the y-axis on the positive side which means you have to double the area result since the curve is symetrical on the y-axis.

Now we integrate;

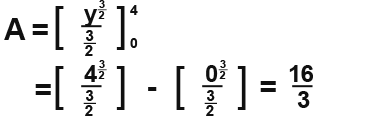
The final area becomes;

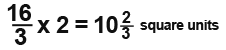
And that’s how you find the area between a curve and the y-axis. It’s really very simple. Remember to find the x equation from the given function by making x the subject and then integrating x within the given lower and upper y-axis.