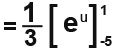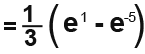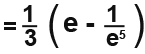Integration by substitution
One form of integration is the integration by inspection method which I have covered here. It might be best for your benefit to go through that revision before attempting this reading, it might make the all proccess easier. Although you can carry out integration by inspection as well, there are some integrals which cannot be integrated this way for example;
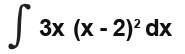
For these type of integrals such as the above we use the method known as integration bu substitution. This method can be very tricky but the more time you spend looking at the examples the more you improve on the logic behind it.So just spend more time on. The method of integration by substitution is exactly what it sounds. It involves setting up a new variable which in most cases is referenced by u to simplify the integral in terms of u and then integrating the new integral. It is very simple.
Example 1
Here is a very quick and simple one to start with;
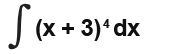
let our new variable u=x+2 So the integral becomes;
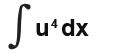
Next we need to rewrite all the parts of the integral in terms of u including the dx you see at the end.
We know that u = x +3 … this must mean that;
![]()
We need to rewrite dx in terms of du, this forms;
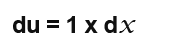
Now we need to replace dx with du. We know taht u = 2x+1;

So our integral becomes;
[IMAGE]
And then we integrate;
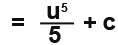
We know that u = x+3, so for completion the integration becomes;
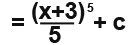
Example 2
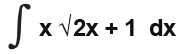
This can be a bit tricky… First identify the u which in most cases will be obvious. Notice we have left out x so the integral is really is;
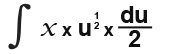
[IMAGE]
We also need to rewrite the remaining x in terms of u we know that u = 2x+1, so;
[IMAGE]
Now the integral becomes;
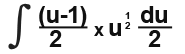
We have replaced x now we need to simplify. This is where you simplifying skills come to good use. Being able to simplify to the simpliest form possible will save you with these kind of mathematical problems. The integral now becomes;
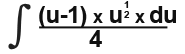
We move the function outside to simplify;
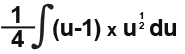

Now we integrate;
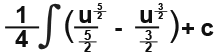
Again simplify;

Now replace the u variables.
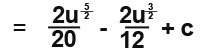
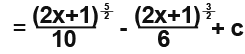
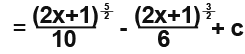
Example 3
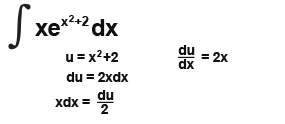
Our integral now becomes;
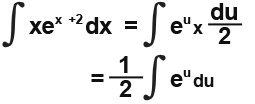
Now we integrate;
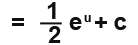
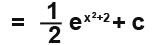
Definite integrals
You can also integrate definite integrals by changing the limits as well. This is a very little advancement from the above but the concept is the same.
Example
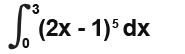
We know that;

Now we need to change the limits as well as previous, we know that u = 2x-1 so;
| x | 0 | 3 |
|---|---|---|
| u=2x-1 | -1 | 5 |
The new limits are u = -1 and u = 5.
So our integral becomes;
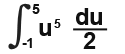
We integrate and subsititute in the limits we have found.
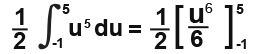
[IMAGE]
Example 2
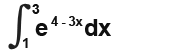
We know that;
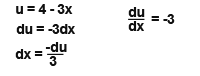
We need to change the limits as well it’s easier to find these with the help of a table as below;
| x | 1 | 3 |
|---|---|---|
| u=4-3x | 1 | -5 |
So our integral becomes;
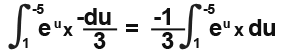
Since we have a negative out side we can swap the limits to get rid of it.
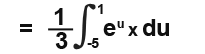
Finally we intehrate and subsititute in the limits.