Adding Algebraic Fractions
Adding numeric fractions
Below we have two fractions separated by an addition sign. We need to add these fractions together.
When given such a problem we first need to find the common denominator. We find this by multiplying the fraction denominators together.
Now we get;
Notice by finding the common denominator we assume that each fraction increased. We multiplied 5×4 to get 20 and we multiplied 4 by 5 to get 20 which is the common denominator. This must mean we need to multiply the numerators by whatever values we multiplied with the denominators as shown below;
We simplify and we get;
Adding simple Algebraic fractions
Work out the following fraction addition;
When adding algebraic fractions the steps are the same as above, below we have an addition of algebraic fractions;
As we did above we find the common denominator first as shown below;
…which means…
We apply the multiplication to the numerators as well as shown below;
And lastly we simplify the expression;
Fractions with linear denominators
Below we have fractions with linear denominators;
We have to find the common denominators first as shown below;
We simplify multiply the two fraction denominators together. Then we rearrange the fractions line the following;
What we did to the denominators must be done to the numerators;
Lastly we expand the brackets and simplify
Denominators with a common factor
The denominators above contain a factor. This factor is (x+3). When form common a denominator any factor that appears in both fraction denominators must only be shown once in the common denominator. The common denominator becomes;
Notice we’ve multiplies the denominators and made sure that we don’t multiply the (x+3) which appears in both denominators, instead we’ve used it only once. Because we’ve multiplied the denominators to find the common denominators we need to do the same for the numerators. We multiplied x by (x+3)(x+5) to find the common denominator that must mean we need to multiply 4x by x as shown below;
We multiplied x(x+3) by (x+5) to get the common denominator x(x+3)(x+5) that must mean we have to do the same to the numerator. Thus we get;
Now we need to simplify it into;
Fractions with quadratic denominators
When given to add fractions with quadratic denominators you may have to factorise first before finding the common denominator. Suppose we wanted toad the fractions below;
First we factorise the denominators as shown below;
Now we need to find lowest common denominator. We can see that both denominators have a factor of (x+2). We need to include this once in the common denominator. So the lowest common denominator is;
This we get;
What we have done to the denominators must be done to the numerators, here we get;
Now we need to expand the brackets as shown below;
And finally we simplify the expression as shown below;
The above becomes the final answer for the addition question.
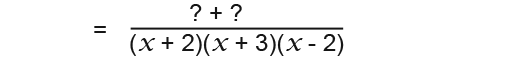
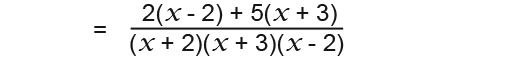
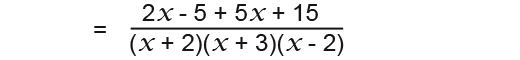
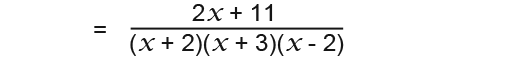

Mali-mali