Angles of elevation and depression
This chapter explores angles of elevation and depression. It covers working with angles of elevation and depression and using scale drawing and trigonometry to calculate heights of tall objects. No prior knowledge is required for this chapter.
Engineers use trigonometry to work out very high heights such as a tree and tall buildings. The following image shows an old chimney. Engineers need to work out how tall it is;
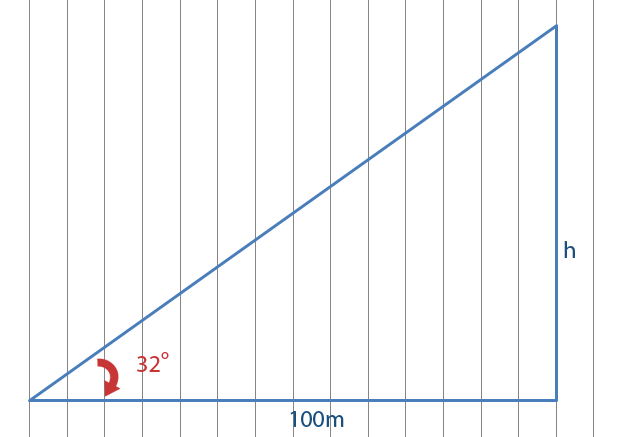
The engineers stand 100m from the chimney. They measure the angle of elevation shown below using a theodolite.
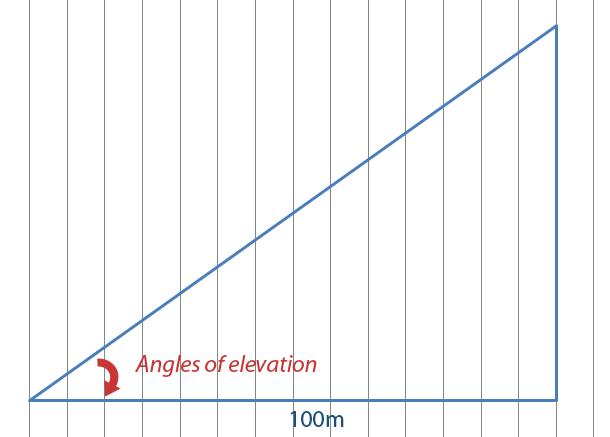
They find out that the angle of elevation is 32°. Suppose they wanted to work out the height.
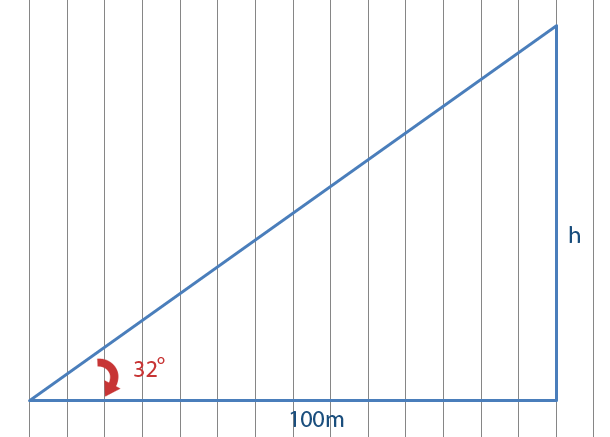
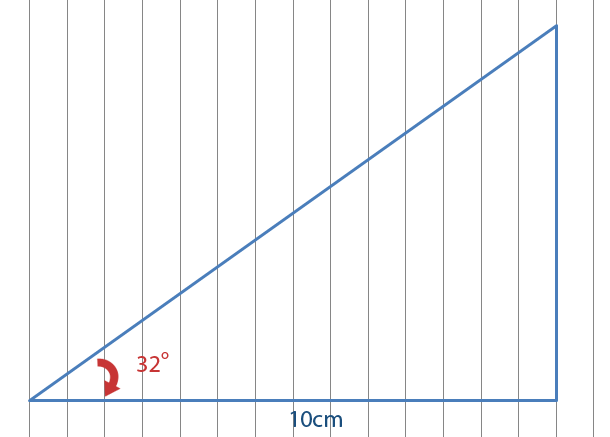
One way to work out the height of the chimney is to so a scale drawing. We could use a scale of 1cm for 10m. First we draw a line 10cm long.

Then we draw an angle of 32 ° as shown below.
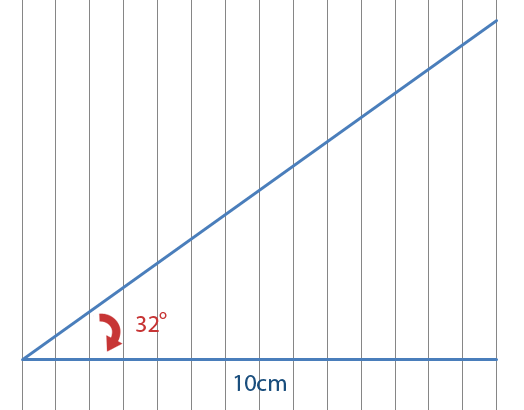
Then we join the height.
Finally we measured the height using a ruler. You’ll find that it is 6.3cm.
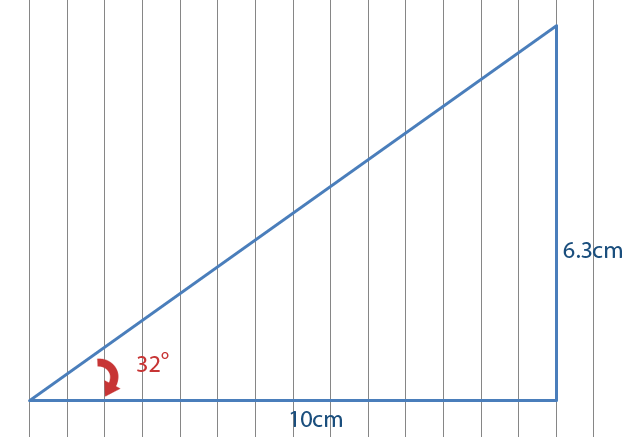
6.3cm represents 63metres in the scaling above. We have found out that the chimney is 63m high.
Trigonometry
We could use a more accurate approach to solve the problem above. We would use trigonometry. The problem above is shown below.
We could use;
![]()
The first step is identifying the known sides. We know the opposite and adjacent.
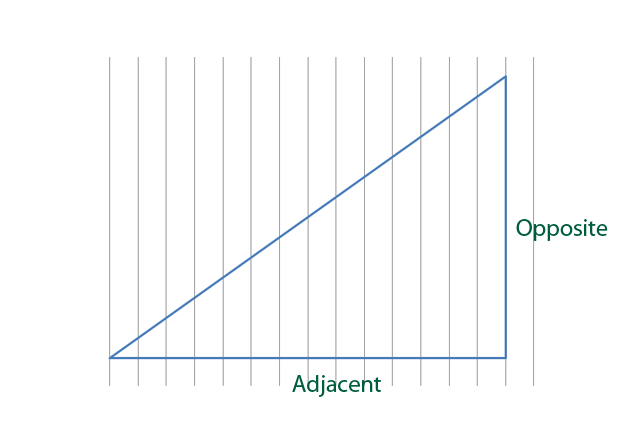
…h is the opposite and 100 is the adjacent.
The second step is identifying the tangent function that we need to use. Using SOHCAHTOA we can use that we need to use tangent.
![]()
The formula for tangent is;

Next we substitute in the values;
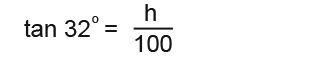
Then we rearrange to get h on it’s own.
![]()
Then we work out 100xtan32° on the calculator and round it off to 1d.p.
![]()
Here we can see that the height of the chimney is 6.25metres.
Angles of depression
John is standing on the edge of a cliff. He sees a boat at sea and wonders how far away it is;

He is aware that the cliff is 40m high.

He measures the angle of depression and finds it is 25°.

Suppose he wanted to find the distance to the boat. Below is a diagram which we can form from the problem to help solve it.
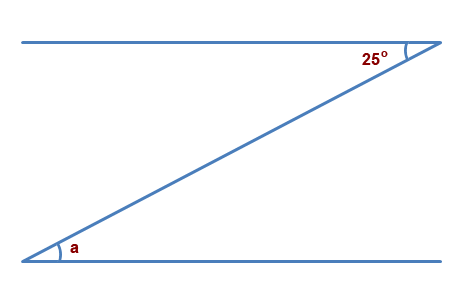
If the angle of depression is 25° that must mean that angle a is 25°
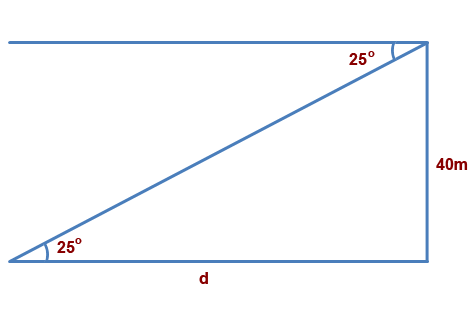
Now we don’t need the angle of depression since the inner angle is known. We would use SOHCAHTOA to solve the problem.
First we identify the sides we know. We have the opposite and adjacent.
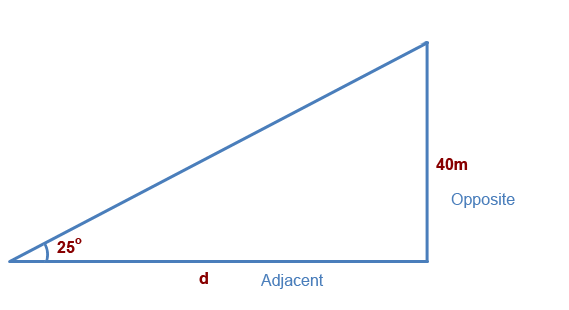
Next we identify the function we need to use from SOHCAHTOA, we can see that;

Next we substitute in the known values.
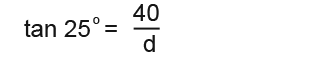
The we rearrange the formula to get;

If you workout 40÷tan25° on the calculator and round off to 1d.p you get;
![]()
We have seen that the distance of the boat is 85.8 m
