Averages

This is an entry which explores averages. In this entry I shall be showing you how to work with averages. You shall learn how to find the mode, median, and mean for a list of data. You will also learn the advantages and disadvantages of each type of averages, and lastly how to find the median and mode from a frequency table. I will assume you’re an absolute beginner.
Averages are used to compare or analyse data. They help us understand the data that we’ve collected to enable use to make the right decisions or conclusions for example; Jane decides to collect data for the cost of a popular orange juice called Mucha. Here are the results of her data.


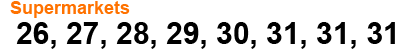
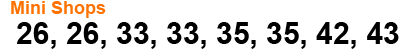
Then she decides to compare the prices from the data she has found. She can compare the mode, median and the mean in her data.

Mode

The mode is the most/popular value in the data. This is the value which occurs most frequently. Here is the data that Jane collected.

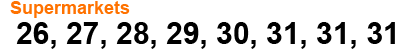
In this data 31p is the mode as it is the most popular cost value in the list of data. The values occur twice as you can see.

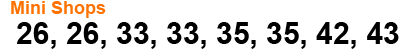
In this data list the values that occur most frequent are 33p and 35. We can call these both the mode. They both occur twice. This is called Bimodal Distribution
The mode is only useful when there items which appear frequently or more than once. You cannot use the mode or try to find it when all the values in the data are different. It is the only average you can find for qualitative data. An example of qualitative data is eye colours.

Median

The median is the middle value in a list of data, population or a probability distribution. This is the numerical value separating the higher half of the data from the lower half. To find the median data has to be placed or listed in order. For example here is the data that Jane collected in order.

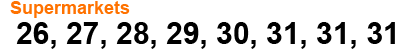
To find the median in this ordered data we cross off a pair of numbers from both ends of the data, one value from each end at a time as shown below.

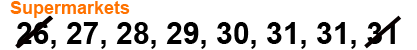
We cross off until we reach the centre most values.

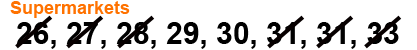
In the crossing above we can see that there are two values in the centre. So we write the middle point of these values as the median. So the median for the super markets data is 29.5

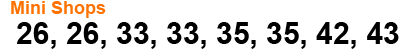
Here we go through the same process as above. First we list the data in order and then we cross out from each end towards the centre as shown below.

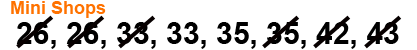
Here we have two values at the centre again, so we write the midpoint of these values. The median for the mini shops data is 34p.
The median is not distorted by extreme values, but that’s because it does not take all the data into account.

Finding the position of median

There other much quicker ways to find the median value. We know that the median is the middle value of an ordered list for example if we had 5 items in a list of data.

In the above list, it is the 3rd item which is the median. To find the median much quicker we can use the following formula or rule.

For example from the list above there are 5 items so;

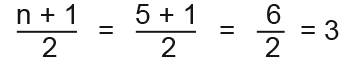
We have been able to find the 3rd item as the median value very quickly by using this method.

Mean

The mean of data is the total of all the data divided by the number of items in that data. The mean is found by this formula;

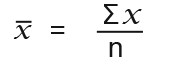
…where;
n is the number of items in the collected data.
x This simply represents each item in the data
Σ This is the Greek letter Sigma which means sum or add, so in this case Σx means total of the values of x.
SYMBOL is the symbol for the mean.
Lets try to find the mean of Jane’s data.

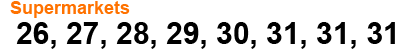
Here n=8 and Σx =335 so the SYMBOL (mean) is;


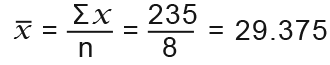
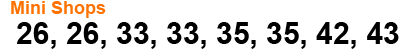
Here n=8 and Σx =273 so SYMBOL (mean) is;

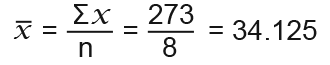
The mean takes into account all the data but can be affected by extremely high values.