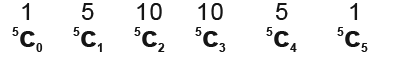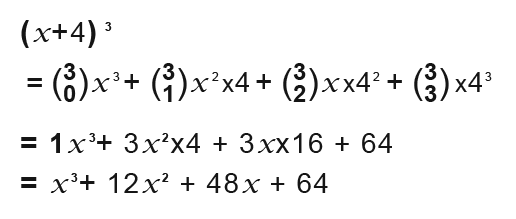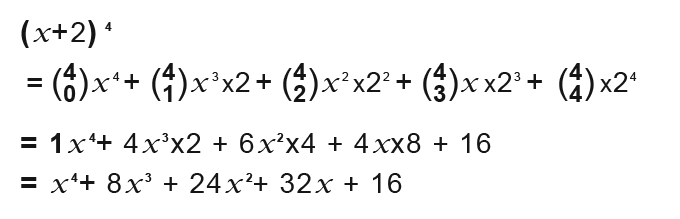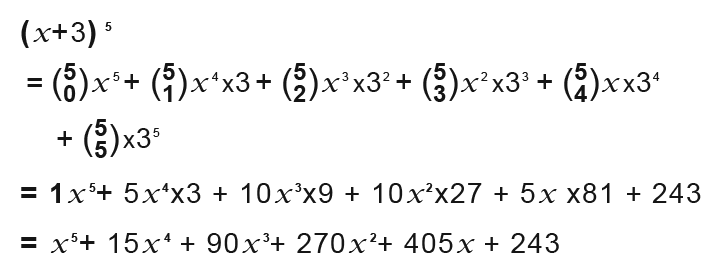Binomial Expansion

This is a continuation from the Pascal’s triangle lesson. It would be good for your benefit to go through it before attempting this.
The numbers in Pascal’s triangle can be generated using the following notation or formula;

You might be able to find it on some calculators. Here are sets of numbers you can find in rows of in the Pascal’s triangle.

5th row

6th row

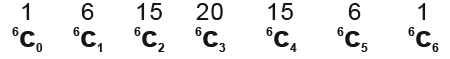
Note how where the row number such as 5th row and the position are on the C

What is ⁿC_r?

The notation ⁿC_r is often used in statistics ⁿC_r is the number of ways of choosing r objects from a group of n objects. For example, the number of ways of picking 2 people from a group of 5 is;
⁵C₂ = 10
This can also be found this way without the calculator;


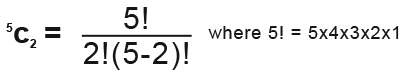
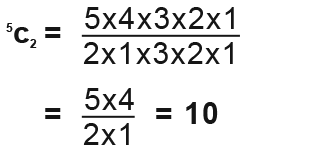
So we can form a general rule here;

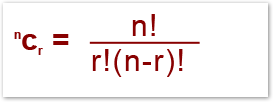
We can also write ⁿC_r as;

The binomial expansion of (a+b)ⁿ is given by;

When ⁿC_r is written as the expansion becomes;

Example

Expand (x+4)₃

Example2

Expand (x+2)₄

Example 3

Expand (x+3)₅

Other cases

You might be asked the coefficient of a specific x within an expansion for example;
Find the coefficient of x⁴ in the expansion of (1+x)⁶.
This is simple. The term with x⁴ in it is;

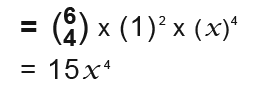
So the coefficient of x⁴ in the expansion of (1+x)⁶ is 15.

Binomial expansion for approximations

You can use binomial expansion for approximations for example;
Work out an approximation for the value (1.003)⁵ using the binomial expansion.
Let us first write (1.003)⁵ as; (1+0.003)⁵.
We don’t need to carry out the all expansion because after the first few terms, the terms get very very small. So we ignore them. We shall do the first 3 terms.

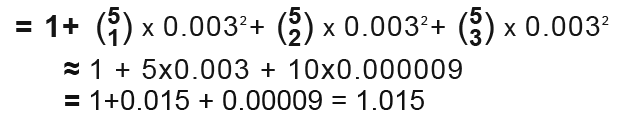
You can try to check on your calculator for (1.003)⁵ you will get 1.0150902780, our approximation is good.