Cosine Rule
In this chapter we shall be exploring the cosine rule. In trigonometry we can use the cosine rule to find the missing sides and angles in a triangle. You must have some basic knowledge of trigonometry and bearings to appreciate this chapter.
Deriving the cosine rule
Let us have a look at how the cosine rule was found or derived. Here is a triangle;
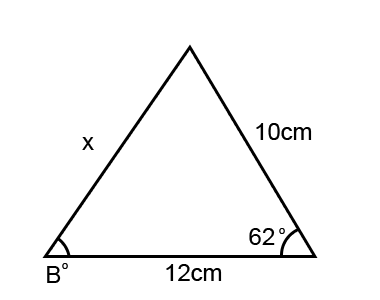
The problem with this triangle is that we cannot solve x using the sine rule because we have one pair or x/sin62°, we have no other pair to equal this to. We can’t use Pythagoras because this is not a right angled triangle. But we can take advantage of Pythagoras.
First draw a line in between the triangle perpendicular to the line AB from C; and create another point D as shown below;
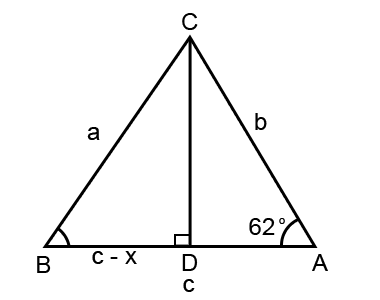
Let’s label DA x. Sine DA is x that must mean that BD is equal to c-x. We have a right angle triangle ACD so we can use Pythagoras here.
![]()
and
![]()
We also have another right angled triangle BCD. So we can use Pythagoras on that as well.
![]()
and
![]()
Notice we have found two equations for CD2 so let’s take these two equations and make them equal to each other.
![]()
Expand the brackets and simplify to find b2.
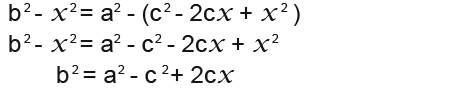
And do the same for a2 to get’
![]()
Let’s look at the triangle ACD again, notice that;

…which means;

Substitute this into the a2 equation we found above and we shall get;
![]()
![]()
The above is the first version rule of the cosine rule.
To find the second rule we just replace the x value in the b2 equation as we have just done to get;
![]()
So the cosine rules corresponding to the following triangle shape are;
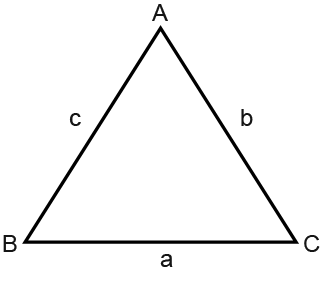

Let’s try finding sides using the above rules below;
Finding sides
In the following examples we shall be finding the value of x when it is opposite the angle and when x is adjacent to the angle;
Example 1
Find the value of x (Opposite the angle)
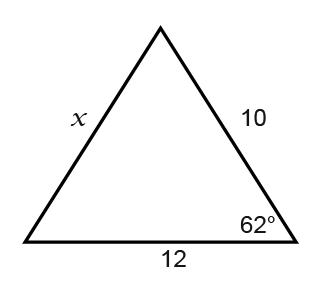
Let’s start by labelling the triangle then use the cosine rule;
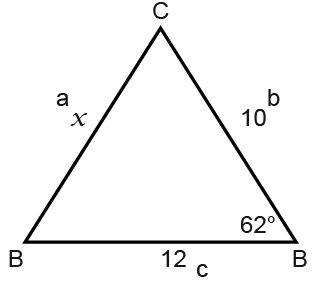
The cosine rule as we discovered above is;
![]()
We substitute in the know values;
![]()
Now we solve to find the value of x. Remember you have to take into account x2. We only want the value of x.

Example 2
Find the length of x (adjacent to the angle)
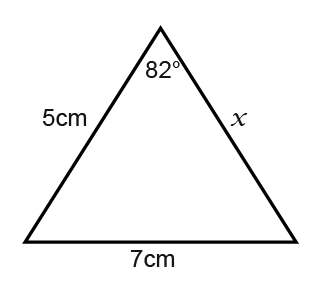
First we label the triangle as we did in the first example. Make good practice of it.
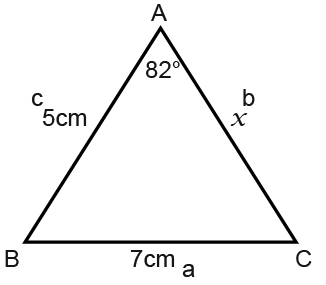
The cosine rule formula to use is;
![]()
We substitute in the known values into the formula;
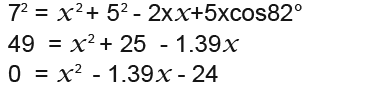
Here we can use the quadratic formula to find the value of x.
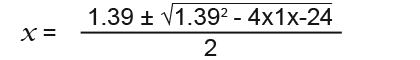
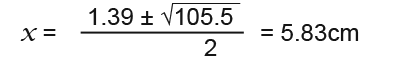
We could have also found the value of x by using the sine rule to find the angle C and then find B using angles in a triangle and then finally with B as the angle;
![]()
Finding sides
Above we have been finding the sides on the triangle. Now we shall explore finding the angles of a triangle.
If we know the 3 sides of the triangle we can use the cosine rule to find any of the angles. Here is a triangle with 3 know sides.
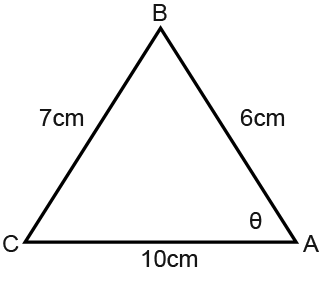
Here we can rearrange the cosine rule to make cosA the subject and then undo the cosine. This is the cosine formula;
![]()
Rearrange to find cosA;
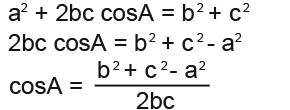
Now we substitute in the known values in our example to solve;
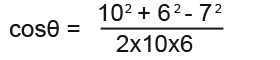
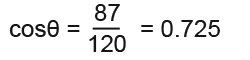
Now we undo the cosine to find the angle at A.

The angle at A as we have found is 43.5.
Example2
Here is another example for finding the angles using the cosine rule.
Find the θ in this triangle.
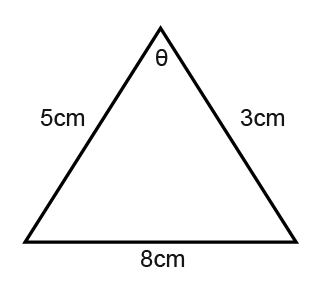
First we label the triangle to correspond to the cosine rule;
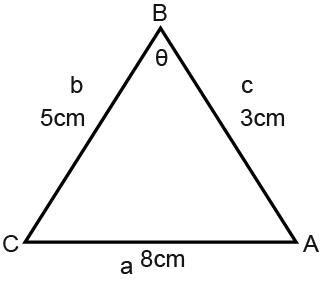
We use the cosine formula but we need to rearrange it such that cosA is the subject.
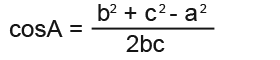
Now we substitute in the known values;
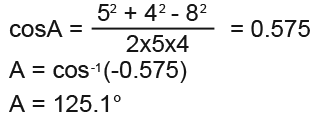
The angle at A is 125.1° which is an obtuse angle;
