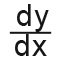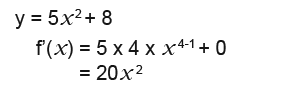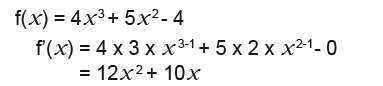Differentiating
In this topic I’ll be concentrating on differentiating polynomials. To differentiate a function means to find the gradient of the function, that is finding the difference between the y-axis dy and dividing it with the difference of the x-axis dx. We can write this as;
Another way to write dy/dx for a function in the form of f(x) is f'(x), so;
To make the topic short; In general if you have a function such as;
y = xn
The formula for the gradient of the function is;
f'(x) = nxn-1
Remember that f'(x) is the same as dy/dx.
In the following table we have the functions and the formulas to find their gradients.
| Function, f(x) | Gradient forumula f'(x) |
|---|---|
| x2 | 2x |
| x3 | 3x2 |
| x4 | 4x3 |
| x5 | 5x4 |
For example
Suppose we have the function y = x2, what would be the gradient?
We know that f'(x) = nxn-1
So;
f'(x) = 2x2-1
= 2x1 = 2x
Example 2
Example 3
Example 4
![]()
First write the function on a single line.
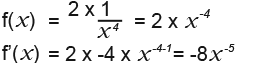
Example 5
![]()
Again first write the function on a single line.
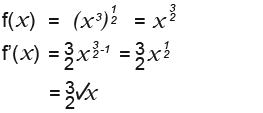
And that’s how you differentiate polynomials. Also remember when y is equal to a number such as y = 6 then f'(x) = 0. This is because this type of function results in a straight line along the y-axis and a straight line has no gradient at all. To think about this you have to think about the simple straight line of a linear graph.