Differentiation notes
This section contains useful notes for differentiation.
- The gradient of a curve y=f(x) at a specific point is equal to the gradient of the tangent to the curve at that point.
- The gradient of the tangent at any particular point is the rate of change of y with respect to x.
- The gradient formula for y=f(x) is given by the equation gradient = f’(x) where f’(x) is called the derived function.
- If f(x) = xn, then f’(x) = nxn-1
- The gradient of a curve can also be represented by dy/dx.
- dy/dx is called the derivative of y with respect to x and the process of finding dy/dx when y is given is called differentiation.
- y = f(x), dy/dx = f’(x)

- y=xn, dy/dx = nxn-1 for all real values of n.
- It can also be shown that if y = axn where a is a constant, then;
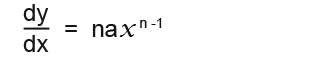
- If y=f(x) ± g(x) then…
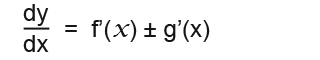
- A second order derivative is written as;
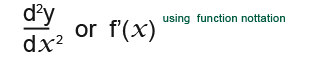
- You can find the rate of change of a function f at a particular point by using f’(x) and substituting in the value of x.
- The equation of the tangent to the curve y=f(x) at point A, (a, f(a))
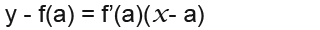
- The equation of the normal to the curve y=f(x) at point A, (a, f(a)) is;
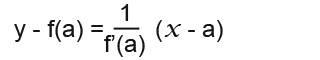

1 Response
[…] http://www.mathsrev.com/differentiation-notes/ […]