Differentiation of Logarithmic Functions

You can find derivatives for logarithms functions as well. Here is the first rule that will help you when working with such functions. It will be best to your advantage to be very familiar with the Chain and Product rule.

The derivative of Inx is 1/x

Example

Find the derivative of f(x) = lnx

Our first example is really simple and straight forward. We know that the derivative of lnx is 1/x so;

Example 2

Find the derivative of f(x) = xlnx
These form of functions require to use the product rule and you will have the result as;

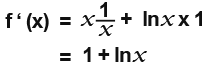
Example 3

Find the derivative of f(x) = ln(x² + 1)
This form of function will require the chain rule. You can read more about the chain rule here.

Example 4

This looks like it’s impossible to differentiate but it’s actually simple. It’s just a mire rearrangement of the function. We can take advantage of the logarithmic rules if you remember. Subtraction of two logarithmic results in division, so we reverse our function.

Now we find the derivative for each component;

We need to simplify it by finding the common denominator as we do with normal fractions;

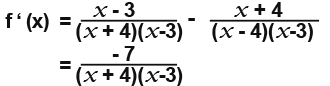
And that is how you work with differentiation of logarithmic functions.