Differentiation of Trigonometric Functions

When differentiating trigonometric functions, here are some of the rules that you should know;

All the above derivatives can be proved and as you continue to expand your knowledge on differentiating these type of functions you’ll be able to prove it. I will prove some of the derivatives for the functions above below.
You can also apply the chain, quotient and product rules when differentiating trigonometric functions.

For example:

Differentiate the trigonometric function 5sinx
To solve this we need to take into account the above rules, here the function involves sinx. That means;
f'(x) = 5 x cosx = 5cosx
It is as simple as that, because know that when we differentiate sinx we get cosx.

Example 2

Differentiate the function 3ex – 5 cosx
f'(x) = 3e^x – (5 x -sinx)
= 3e^x – (-5sinx)
= 3e^x + 5sinx

Differentiating tanx

The trigonometric identities apply here. This is example I will also be proving that the derivative of tanx = sec2x. For example; y = tan x.
We know that we can rewrite tanx using sinx and cosx.

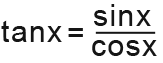
Since this is a fraction we will have to use the quotient rule.

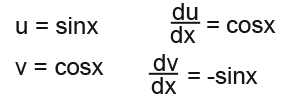
We then use the quotient rule since we now know the values for the letters in the rule.

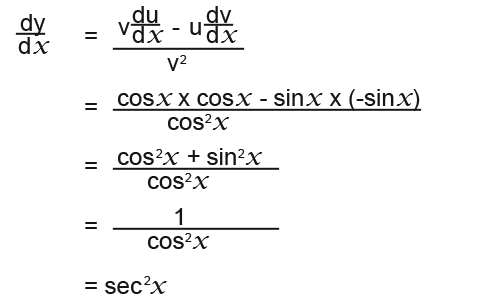
So now we know that if;
y = tanx then f'(x) = sec²x