Double Angle Formulae

In this chapter we shall be looking at the double angle formulae. We shall explore the double angle formulae for sin2A, cos2A and tan2A and then use them to solve equations and simplify expressions involving multiple angles. You must have prior knowledge of the addition formulae to appreciate this topic.

Deriving the double angle formulae

Here we shall derive the double angle formulae using the addition formulae. We shall need to write A+B as A+A.

sin 2A

For this we expand 2A to get A+A so;

Now we use the addition formula to get;

…when simplified we get;

So; sin2A = 2sinAcosB

cos2A

Again here we expand the 2A into A+A and us the addition formulae so;

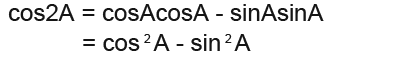
You must know that sin²A + cos²A = 1 We replace cos²A with 1-sin²A as follows;

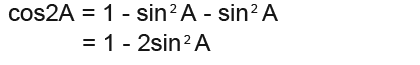
Also sin²A = 1-cos²A which means;

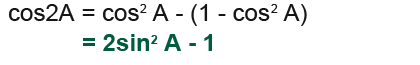
Here we have found 3 expressions for cos2A.

tan2A

Expand 2A again into A+A;

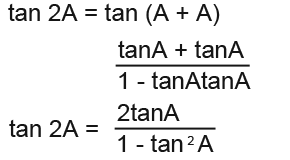
So the double angle formulae are;

Solving equations using double angle formulae

We can use the double angle formulae to solve equations as shown below.

Example

Solve: 3sin2θ = 2sinθ for 0° ≤ θ ≤ 360°
Here are the two graphs of y=3sin2 θ and y=2sin θ which are shown below. We have to find the angels at which these curves intersect between x=0° and x =360°;

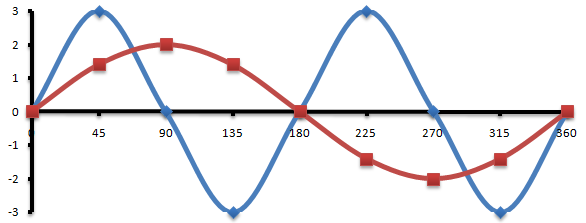
On the graph we can see some of these angles at which the two curves intersect, for example we see 0°, 180° and 360°. That’s not all. So;

Let’s use the double angle formula for sin2θ° = 2sin0cosθ° so;



Simplify and factorise;

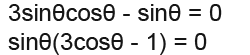
Now we have;

For sinθ = 0;

For 3cos θ – 1 = 0;


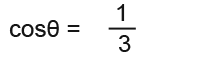
So the angles where the two lines intersect are;

We have managed to find all the angles with the help of the double angle formulae instead of drawing out the graphs and looking at where they intersect.

Example 2

cos2 θ = 3sin θ for 0° ≤ θ ≤ 360°
Here is the graph showing both curves

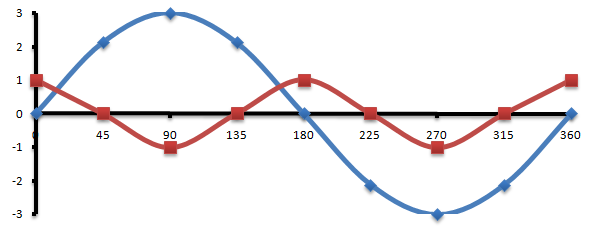
So we have the equation;

We replace cos2θ with 1 – 2sin²θ to get;

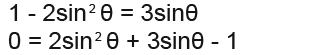
We can’t factorise this so we use the quadratic formula

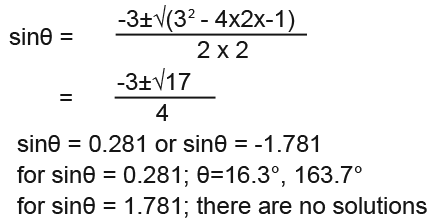
As you see from above there are two angles for the interval we have been asked to find the angles in and that’s exactly what we have found.

Simplifying expressions

We can also use the double angle formulae to simplify expressions such as the ones in the following examples.

Example

Prove that (sin A + cosA)² = 1 + sin2A.
When we expand (sin A + cosA)² we get;

Using the double angle formulae we can see that;
1 = sin²A + cos²A and sin2A = 2sinAcosA
So we replace sin²A + cos²A with 1 and 2sinAcosA with sin2A to get;

That proves the expression.

Example 2

Prove that;

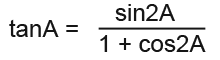
Expand the right hand-side. We know that cos2A = 2cos²A – 1 in the double angle formula. So;

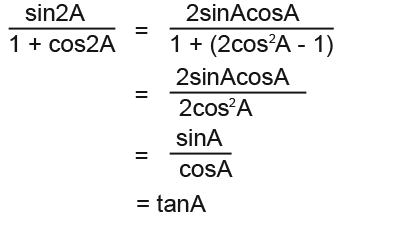
That proves the expression using the double angle formulae.

Example 3

Prove that;

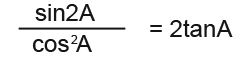
We know that sin2A is sinAcosA in the double angle formulae. We expand the left hand side and cancel out the cosA as shown below;

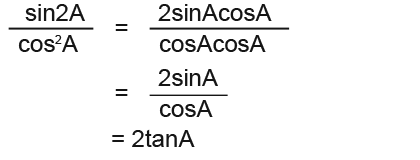
That proves the expression by using the double angle formulae.