Equation of a line

This chapter explores equation of a line. It covers understanding that y – y = m(x = x₁) is the equation of a straight line, finding the equation of a line using gradient and one point, finding the equation of a line using two points. Before attempting this chapter you must have prior knowledge of gradient and midpoint, perpendicular lines, y = mx + c.

Understanding the new equation

You may have known the following equation as the general equation of a straight line is given by;

There is also another general equation that can be even more useful. Let us look at another equation, imagine of a straight line such as that shown below. A general point has been shown on the line. We shall call it (x, y)

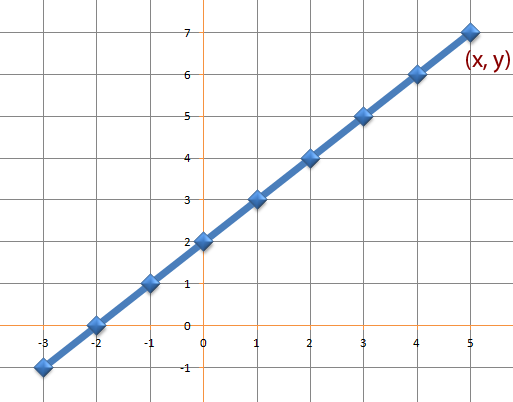
Another point for which we know the coordinates is shown. We shall call it (x, y)

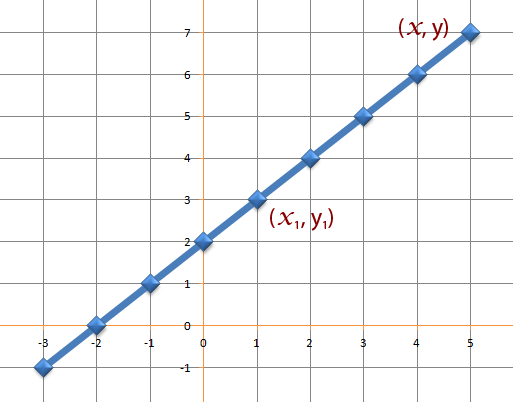
We can work out the gradient m by using the following.

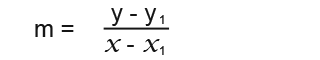
We can rearrange it to form the following;

The above equation is the new version of the equation of a line. m is the gradient (x₁, y¹) is a specified point you are given.

Using gradient and one point

In this section we shall use the formula that we have formed above, The formula was;

…where m is the gradient and (x, y) is a specific point that has been provided.
Suppose we had to find the equation of the line with gradient 2 which passes through the point (1, 3)
We have been been told that m the gradient is 2 and (1, 3) lies on the line meaning;

So the equation becomes;

We can expand the brackets and then rearrange

So the equation that we’re after is;

We can sketch the graph to check it.

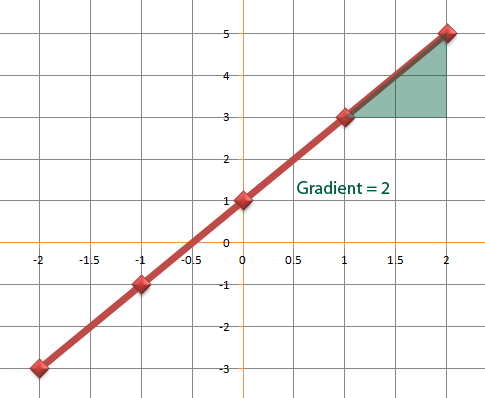
Using two points

We can also use the formula above to find the equation of a line through two given points, Suppose we had to find the equation of the line through (2, 4) and (7, 3)
First we have to find the gradient m to be used in the equation. Gradient is given by the following formula;

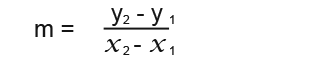
The two given points are;

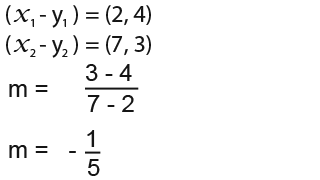
We now know the gradient so we can use it in the formula with;

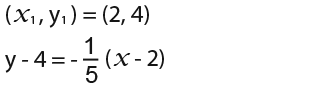
To make the equation simple we get rid of the fraction.

Remember we have negative which has to be taken into account when simplifying further;

We can now rearrange to form the equation as shown below.

Exam question

Here is an exam question that we could try out.
Find the perpendicular bisector of the line joining P(-4, 5) to Q(2, 3)
First let us draw a sketch to help observe what is going on.

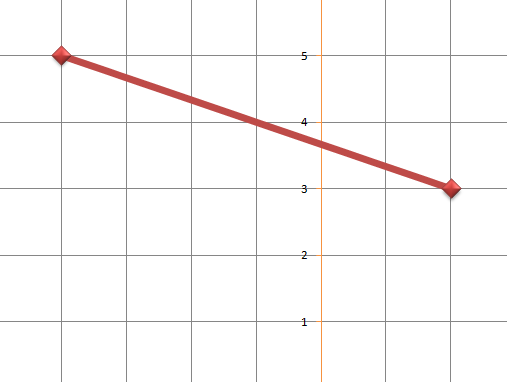
The perpendicular bisector is the line at the right angles to PQ which cuts it in half. To find the equation of the new line we need a point on the line and the gradient. The midpoint of PQ lies on the new line. To work out the midpoint we use;

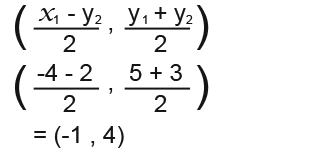
We have managed to find the midpoint. Now we need to work out the gradient of PQ. We use;

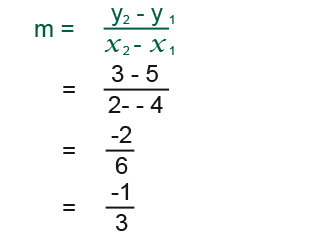
If the gradient of PQ is -1/3 then the gradient of the perpendicular bisector is 3.
Now we can use the following formula;

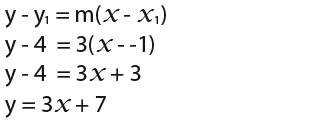
We can conclude that the perpendicular besector equation is;