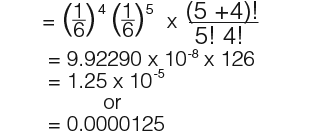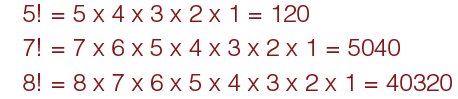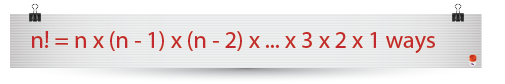Factorials

This section explores factorial notation. Factorials are very popular in many areas of mathematics especially in combinations and permutations. This entry will be useful in the binomial distribution article so adding it first was necessary. In mathematics, a factorial is denoted by;

The factorial of an integer n, is the product of all positive integers less than or equal to n. For example;

You multiply together all the numbers less than n together from n (I.e 5 above) until you get to 1. 5! Is pronounced as “5 factorial”.
It is important to note that the value of 0! is 1, according to the conversation for an empty product.
We can use factorial notation to find the number of arrangement of a list of objects or the number of ways that a certain list of things can be organized in.

Example

Suppose we had a list of 3 balls in three different colours; one red, one blue and the other green.

Then we had to queue the balls in a line ie having red ball first followed by the green and then the blue. We choose one ball at a time.
The first ball that we choose can be chosen in 3 ways since we have 3 balls to start with. The first ball could be red, green or blue.

When we choose the first ball (let us say it happens to be red). There will be 2 possibilities for the second ball. The number of possibilities will still remain the same even if the first ball had been blue.

The third ball can be chosen in only one way;

Here there are 6 ways to arrange the balls in;

3x2x1 can be written as 3! or 3 factorial;

We can list the possible ways the balls can be arranged in a systematic. For instance the first is red…

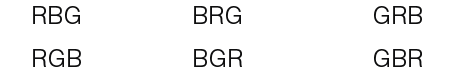
Example

Here is another example of where factorial notation can be used. Suppose we had to find the number of ways that objects can be arranged in where two are red and two are blue.
In this example notice there are only two types of objects, a red and a green and they come in two – to form 4 objects. We must label the two red objects R₁ and R₂ and the two blue objects B₁ and B₂. This will allow us to treat the objects as 4 different objects and therefore 4! ways of rearranging them. You will notice that B₁ B₂ are also identical to arrangements with B₂ B₁… therefore we must divide the total by 2. This is the same as dividing by 2! We will divide by 2! for the 2 reds and 2! for the 2 blues. The number of ways to arrange the objects becomes;

We can list them as follows;

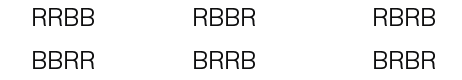
We can formulate a general rule for the number of ways to arrange a given number of objects.

• n different objects can be arranged in;

  

• n objects with a of one type and (n-a) of another can be arranged in;

  

Below are some examples of where these general rules can be used.

Example

In a game John is playing with some identically shaped coloured bricks, and has to find a number of different ways to arrange them. The bricks come in 2 colours; red and green.
Suppose we had to find the number of ways of arranging 5 red and 3 green bricks. The number of ways is given by;

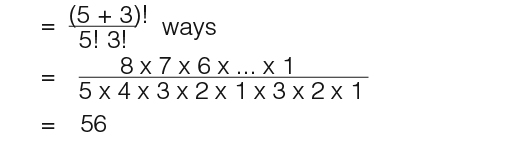
We can also simplify the calculation by working out;

…on the calculator. Notice that;

…because if a = 3 then n-a =6 and vice versa. You can try it on your calculator.
Suppose there were 4 red and 8 green bricks instead to arrange. The number of ways will become;

…which we can also write as;

Example

In this example we shall use probabilities. Suppose a die is rolled 9 times. What would be the probability of getting no sixes, only sixes and, 4 twos and 5 sixes.
For the probability of getting no sixes, we let;

Therefore S’ is the outcome that the die does not land on a six. So;

…we know the probability of getting no six in a single roll is;

…therefore the probability of getting no six in a single roll is;

In 9 rolls the probability of getting no sixes becomes;

For the probability of getting 3 sixes we know that;


…this gives;

And lastly the probability of getting 4 twos and 5 sixes.