Gradient of a Straight Line

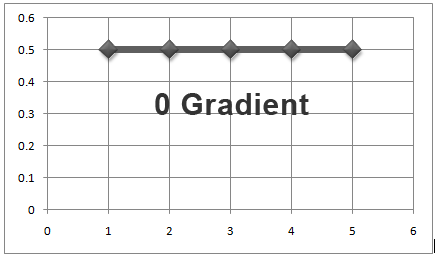
The gradient is the result of the division between the length on the y-axis and the x-axis covered by the line or very simply the value representing the slopeness of the line. Here we’re going to be working with straight lines; for example a straight horizontal line as that shown below has a gradient of zero.

A vertical straight line has an infinite gradient;

A 45 degree to the horizontal line has a gradient of 1;

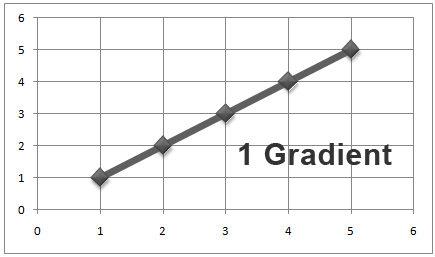
No matter where these lines occur on the graph their gradients will always be the same.

For example

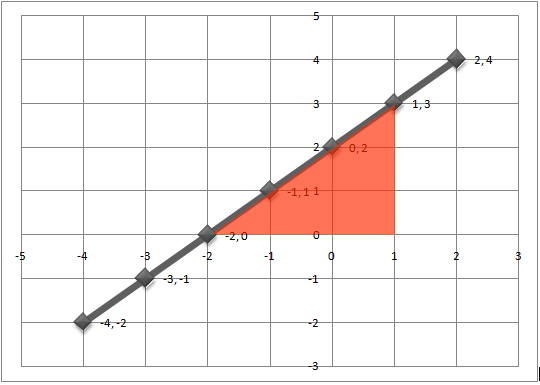
Above we have a graph with a straight line. To find the gradient we draw a triangle under the graph as shown above. So we have;

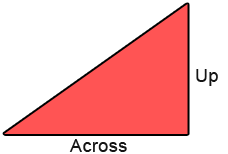
The formula for the gradient becomes;

As already noted, no matter were you draw the triangle or how big or small the gradient will always be the dame since it’s a straight line and the value increments are fixed.

One important rule you must note is that; Downwards slopes are negative while the upwards slopes are positive.

Consider this example;

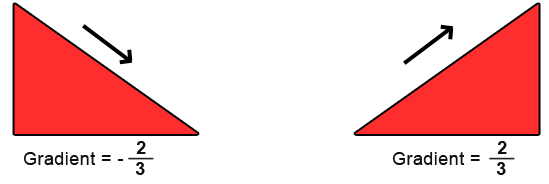
We have two slopes taken from graphs, one is increasing while the other is decreasing. The gradients are the same but the lines are different. In the first diagram the y decreases while the x increases and in the second diagram y increases while x increases.

Example 1

Work out the gradient of the line joining (4, 0) and (-2, 5)

Well here we could work it out the long way. We could draw the graph with the straight line to the get the full picture.

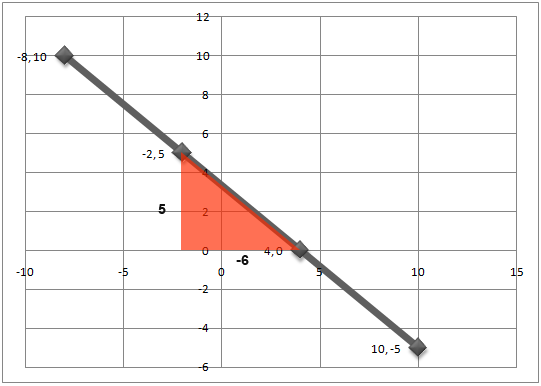
Above is the graph and we’ve drawn a triangle on it to find the gradient. We know that the gradient is found by dividing the difference in x-coordinates with the difference in the y-coordinates (their length to be precise) So;

The difference in the x-coordinates is;
-2-4 = -6

The difference in the y-coordinates is;
5-0 = 5

So the gradient becomes;

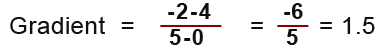
Notice in our results we have a negative which is corresponding to the fact that the gradient of a line towards down results in a negative value.

You might have noticed there is a formula to find the gradient of a straight line, well that formula is;

Gradient Facts

There are some simple gradient facts that you must know;

If two lines have the same gradient they are parallel.

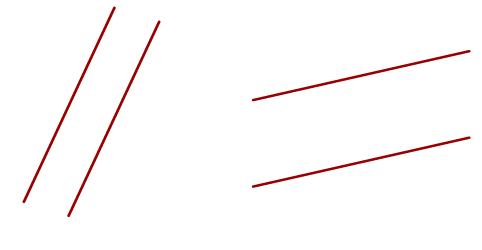
The above lines are parallel and therefore have the same gradient;

Two lines are perpendicular if the angle between them is 90 degrees, for example;

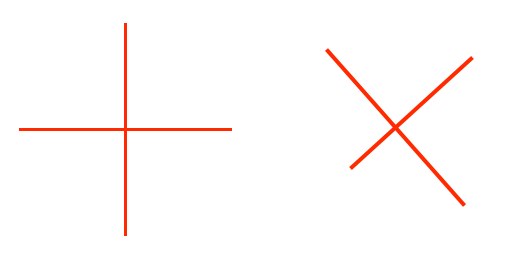
The above lines are crossing each other at 90 degrees and therefore are perpendicular to each other, this is true for all objects.

This is a rule about perpendicular lines, if 2 perpendicular lines have gradients m₁ and m₂ then m₂ is the negative reciprocal of m₁.

For example suppose we have two lines which are perpendicular to each other. If line a has a gradient of 3 then line b must have a gradient of -3 if both lines are perpendicular to each other. The following illustration shows this.