Growth and Decay

Growth

We can model the growth of natural phenomena such as the human population or bacteria growth around an exponential growth formula. The general formula for growth is;

…where A and k are constants and t is time over which the growth takes place.
So when t=0, y=Ae⁰ = A, you must know that any number to the power of 0 results in 1 e⁰ = 1. This means the value of A is the quantity at the start, t=0.
The following graph shows the general appearance of this formula or the exponential growth.

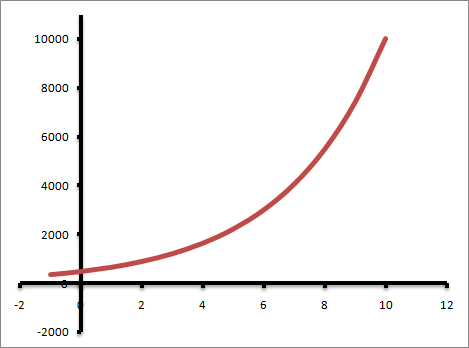
Example

In an experiment a student is told not to wash his hair for a few days which led to bacteria growth. The student’s bacteria growth rate is; y=500e^2t …where t is the time in hours.
The number of bacteria at the start is when t=0 so;

The amount of the bacteria at the start is 500 bacteria.

The amount of bacteria in 24 hours is 3.5×10²³.
Remember y in the formula is the amount of bacteria at different times (t)
Suppose we wanted to find out how long it would take for the bacteria to reach 1 million. y is the bacteria. So we just replace y with 1 million as shown below.

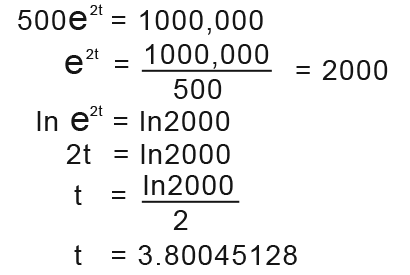
It takes 3.8 hours for the bacteria to reach 1 million.
How about 1 billion? We replace y again and solve…

It takes 7.25 hours for the bacteria to reach 1 billion.

Decay

The same principle applies here except the exponential growth is in the negative direction (getting less) rather than growing.
The general formula for decay involves the function e^-x. The following is the general formula for decay.

The general graphs for decay exhibit the following graph appearance.

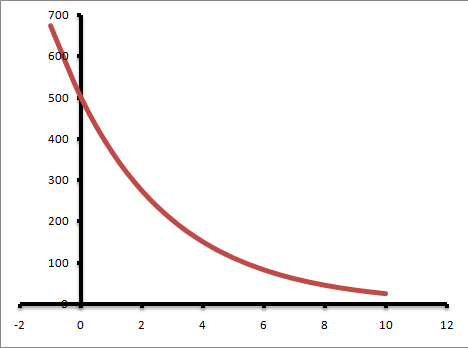
You can see that the graph is improving in the negative direction which shows decay or loss.

Example

The amount of radioactive substance at time t is give by the following formula;

…where R is the amount of substance and t is the time.
• How much radioactive substance is there at the start?
At the start, t=0 so;

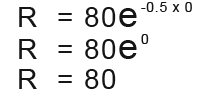
The amount of the radioactive substance at that start is 10.
• What is the halve-life of the substance?
We know that the half-life is the time taken for the amount of the substance to half.

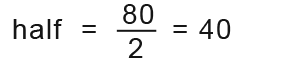
We’re looking for the time when the substance is 40.
That is;

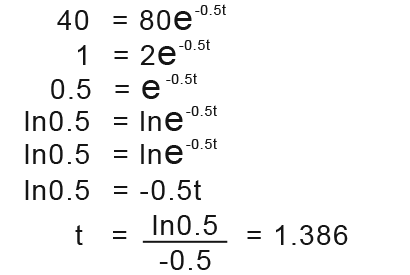
The half-life of the radioactive substance if 1 hour and 39 minutes to the nearest minute.

Example

A disease has involved in a small town wiping out the human population in that area. The number of the human population infected at time t days is;

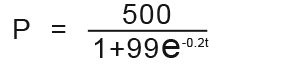
How much of the population is infected after 10 days?
After 10 days t=10 so we replace t in the formula above to fine the number of the population infected during this time;

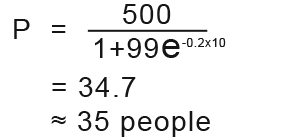
The number of the population infected after 10 days is 10 people.
How long would it take before 400 people get infected?
Here it’s the same process, just place the number in the formula and then workout.

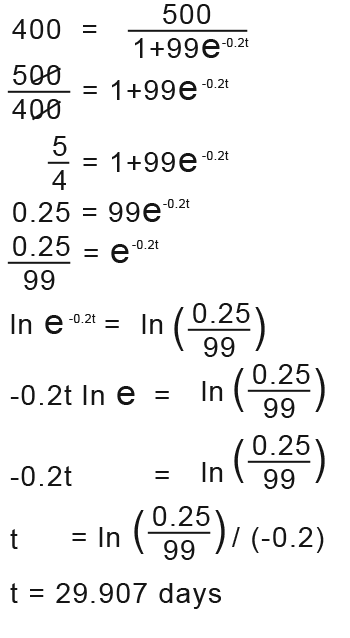
After 29 days 400 people of the population will be infected.