Integration By Parts

This chapter explores integration by parts. You must have prior knowledge of integrating trigonometric functions, e^x and lnx and the product rule.
Integration by parts helps us to integrate more complicated products such as;

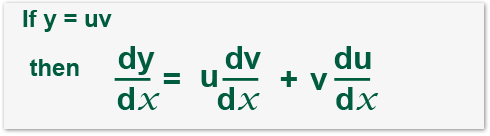
We can’t use the substitution rule since the function x and cosx are not related. A new method we could use is working backwards. Suppose we wanted to differentiate.

It appears that the product rule is applicable here. The product rule is;

Let’s differentiate y = xsinx, let us make;

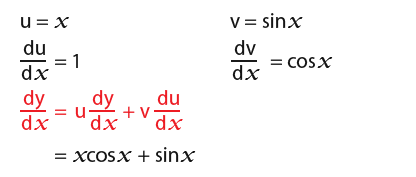
Using the product ruleabove we have found that if y=xsinx then…

It also implies that;

This must mean that;

We know the integral of sinx is –cosx thus we have;

If we rearrange it we get;

Example 2

Here is another example using the backward method we’ve discovered. Suppose we wanted to work out;

If we start with the function y = e^x and try to differentiate using the product rule, Let’s have;

The product rule is;

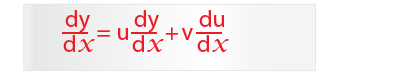
…thus we have;

If we have found that y=xe^x differentiates to;

That must mean that;

Let us split the integral into two parts as shown below;

We know that;

So;

If we rearrange we get…

We have managed to find the answer by differentiating.

Integration by parts formula

Previously we relied on guessing what product to start with and then differentiating it. We can form a formula which can be used instead. Let’s start with a product;

We know that by differentiating we get;

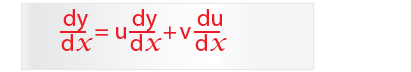
This must mean that;

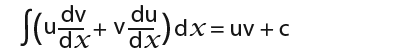
Next we split up the integral as we did before;

If we form…

…the subject then we would get…

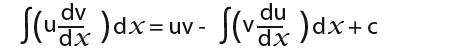
The above is the formula for Integration by parts. That is;

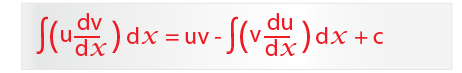
Example

Suppose we wanted to use the integration by parts formula we have to found to integrate;

We need to compare the above with;

We need to decide which part will be u and which part will be dv/dx. Let us make;

When we differentiate u we get;

…and integrate dv/dx to get v.

Now we can substitute the values into the formula;

The we simplify;

Integrate the rest of the part;

Finding the area

Suppose we wanted to find out the area bounded by the curve;

You must know that finding the area is to integrate. Below is the graph of y=sin4x;

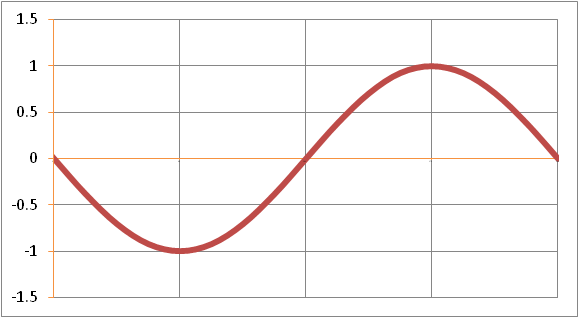
We can see that the graph is positive for all values of x between 0 and π/4. Here we know we don’t have to worry about negatives. That must mean that the area required is simply between the limits 0 and π/4 as shown below;

We can use integration by parts to solve the integral, let use make;

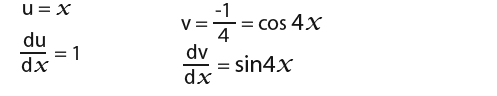
We can substitute this into;

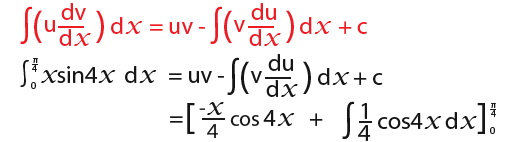
Next we simplify;

Now we can substitute in the limits;

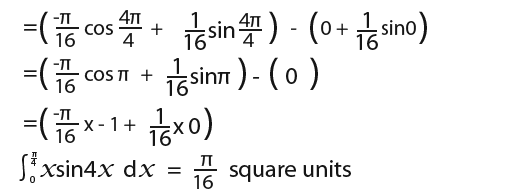
Integrating lnx by parts

Suppose we wanted to integrate;

We know that lnx differentiates to 1/x that is;

That must mean that 1/x integrates to lnx, that is;

We can use integration by parts to integrate lnx.

Let;

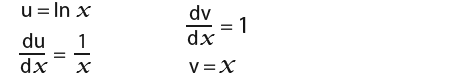
We then use the integration by parts formula;

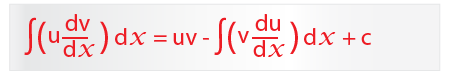
The integral becomes;

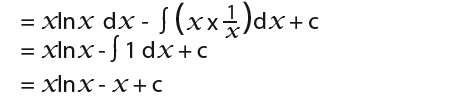
So the answer is;