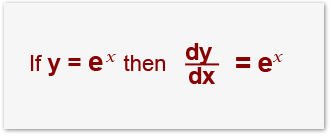In differentiation we know that e^x differentiates to e^x as follows.

Since integration is the opposite of differentiation it must mean that:

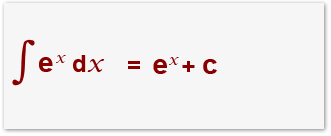
Suppose we wanted to find out the integration e^4x, Think about it logically;

This must mean that:

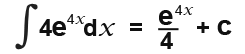
Since we multiplied we must divide. It is as simple as that.
In general…

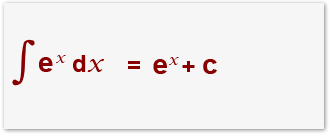
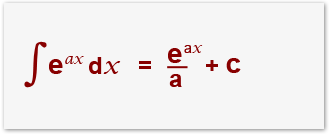
Example

Work out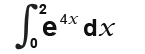
First we integrate

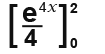
Substitute in the limits and subtract the higher limit from the lower limit as follows.

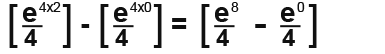
Any number to the power zero is a 1 so e⁰ = 1. Continue.

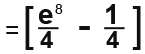
In most cases it’s better to simplify the values or calculations than trying to work out the actual value of the calculation especially with constant numbers, for example;

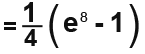
Notice I have just simplified my answer rather than working out the value.

Work out

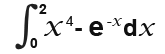
Integrate each term in the equation as follows. You must be careful here with the e^-x, watch how I handle it.

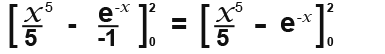
Now substitute in the limits and subtract.

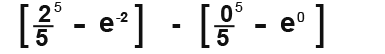
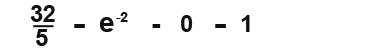
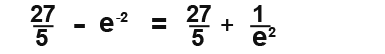
Integration of 1/x into In|x|+c

You must know that x-1 = 1/x. In the following example I shall be showing you how to work with x-1 when integrating. If we try to integrate x-1 in the normal we get the following.

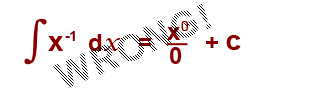
The above expression is and you can’t integrate 1/x this way. We know that:

this must mean:

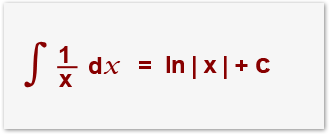
We have written 1/x as ln |x| instead of ln x because ln of a negative number is null or undefined, so can’t be a negative number.

Some integration of this form require some logic, for example;

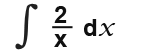
In this case we have to form 1/x. So we take 2 out as a factor and it becomes.


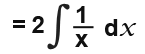
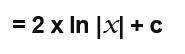
So in general:

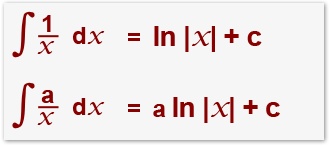
Example:

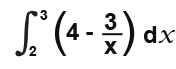
First we integrate every single term separately.

Substitute in the limits and then subtract as follows.

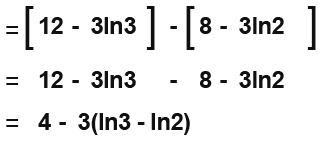
Remember the logarithms rule where;

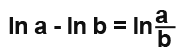
You can read more about the logarithms here, So the answer becomes;

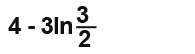
Example:

Work out

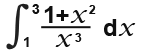
In this case we would have to split the fraction into two because this can’t be integrated in this form. This becomes;

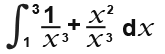
…which simplifies to:

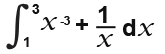
Now we can integrate as normal;

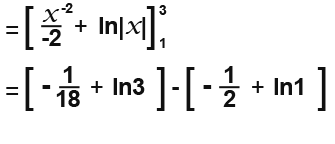
Why don’t you complete this one and check to see whether you’ve learnt how to integrate this.