Intersecting Lines and Curves 1
This section explores intersecting lines and curves. This is the first part of this chapter. It covers finding the intersection of a line and a curve using algebraic methods. It will be useful to have prior knowledge of solving linear simultaneous equations.
Intersecting quadratics and lines using graphs
This section explores intersecting quadratics and lines using graphs. Suppose we wanted to find the intersection of the following curve and line.

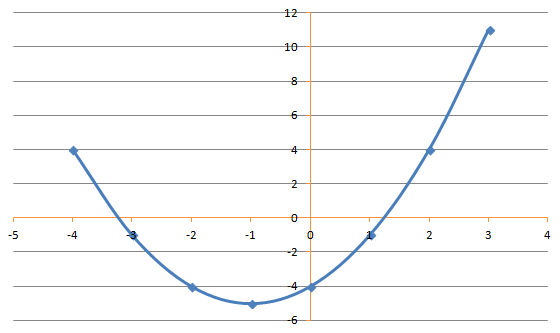
We can use a graph to solve the problem above. First we plot the graph of y=x2 + 2x – 4. But we first need to find the y values, to do that we draw a table such as that shown below.
| x | y = x2 + 2x – 4 |
|---|---|
| -4 | |
| -3 | |
| -2 | |
| -1 | |
| 0 | |
| 1 | |
| 2 | |
| 3 |
We have worked out the values taking x from -4 to 3 and substituting it in the equation starting with x = -4. Below we have plotted the graph.
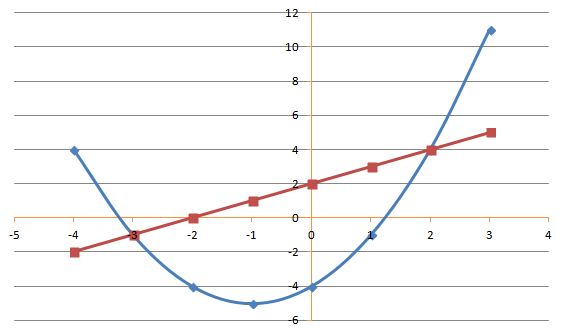
Now we have to plot the line y = x + 2 on top. It must be a straight line and with a gradient of 1 and intercepts at 2. We go through the same steps as above and then draw the line on top as shown below.
![]()
Now we can read off where the line and the curve cross each other. The two points where they intersect is at;
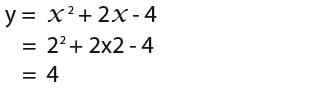
Make sure to check whether the points in both equations provide the same value, for example at (2, 4)
…first we can substitute 2 for x in y = x2 + 2x -4

…then again we substitute 2 for x into y = x + 2 to be correct we have to get 4.

…you can do the same for the other point as well.
Finding the intersection using algebra
We can also use algebra to find the intersection of the curve and the line for example suppowe we wanted to find the intersection of the following curve and line;
![]()
There is a quicker way to solve the problem, this does not involve graphs. Above we saw that while checking out the answer both equations had to have the y values equal to each other to be true. This must mean that the expressions must be equal to each other as shown below.
![]()
The expression have become a quadratic expression which we have to solve. We have to make the right hand side equal to zero. To do that we subtract x and 2 from both sides.
![]()
…that gives;
![]()
Now we can factorise into two brackets.
![]()
So now we have;
![]()
…we find the x values
![]()
We have managed to find the x values now we need to find the y values. To do that we substitute in the original equations. You can use either one, the line is simpler so we shall use that;
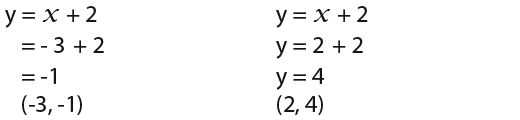
So the two coordinates where the line and the curve intersect are;
![]()
