Radians, Arcs and Areas
This chapter explores radians, arcs, and areas. Before attempting the chapter you must have prior knowledge of finding lengths of arcs and areas of segments using degrees. This chapter explores using radians to measure angles, finding areas of sectors and segments and finding lengths of arcs.
What is a radian?
You may be very familiar in measuring angles using degrees, angles can also be measured in radians. The symbol for radians is c.
One radian has been shown in the arc below. This is where the arc length is the same as the radius.
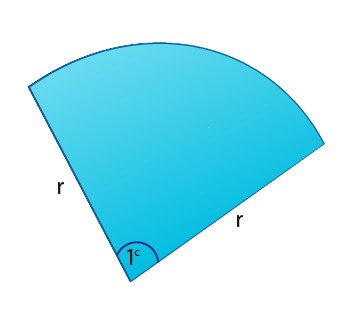
Lets try to find the radian for the above. We know that the arc length is the fraction of the circumference (2π). That is;

In the example above the arc length is the same as the radius that must mean that;
![]()
Since we have r on both sides in the above we can cancel them out to get;
![]()
We can rearrange to make θ the subject;
![]()
We can conclude that;
![]()
…we can also write;
![]()
The above also implies that…

or
![]()
Converting degree to radians
Lets convert angles from degrees to radians. We know that;
![]()
That must mean for the 90° or right angle.
![]()
…and…
![]()
…and…
![]()
…and a full turn of 360°
![]()
You can convert any angle to radians as a fraction π for example.
Example
Convert 44° to radians
…we know that…
![]()
…that must mean…
![]()
…when we simplify we get;
![]()
Above we have found that radian of 44°
We can simply change the degree values of graph to radians, we know that;
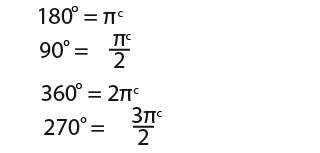
Suppose we wanted to sketch the graph of;
![]()
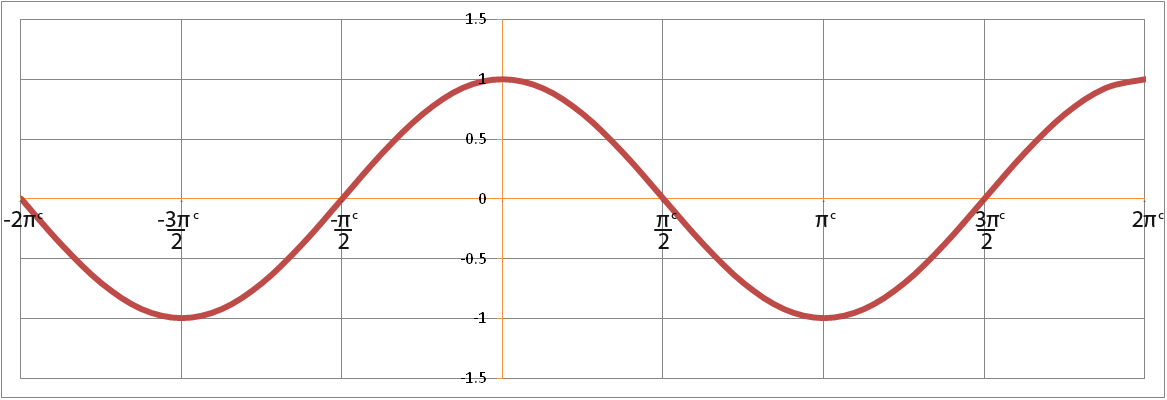
Below is the graph of y=cosθ with the angles labelled in radians.
Trigonometric graphs involving radians
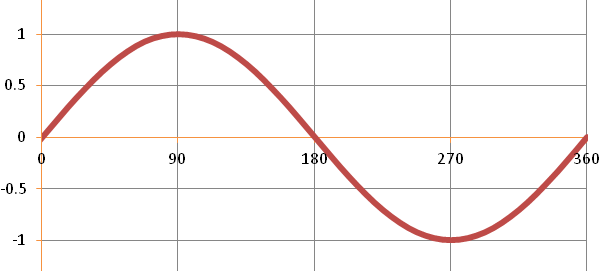
We can also sketch graphs using radians. Below is the graph for y=sinθ whose angles are labelled in degrees.
…and below is the same graph labelled in radians.
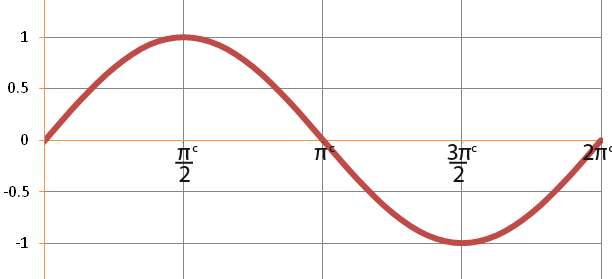
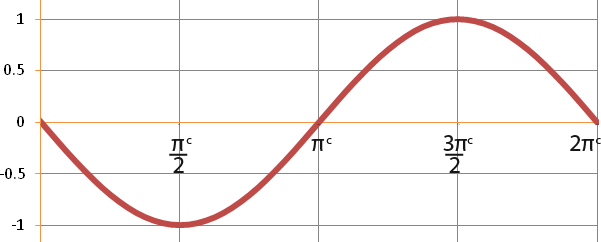
The graph…
![]()
…is the same shape except shifted π/2 to the left. The graph has been shown below.
Arc length and area of sector
Radians are so helpful in making the process of finding arc lengths and areas very easier. The angle shown below is shown in radians, r is the radius of the sector.
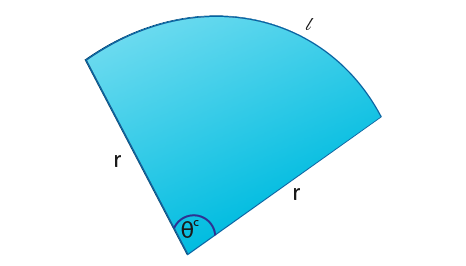
Suppose we wanted to find the arc length.

Remember that 2π° = 360° and 2πr is the circumference of a circle. We can cancel out π’s and 2’s from the equation and the result will be;
![]()
We can form a conclusion that when θ is given in radians.
![]()
It is also very easy to find the area of a sector.
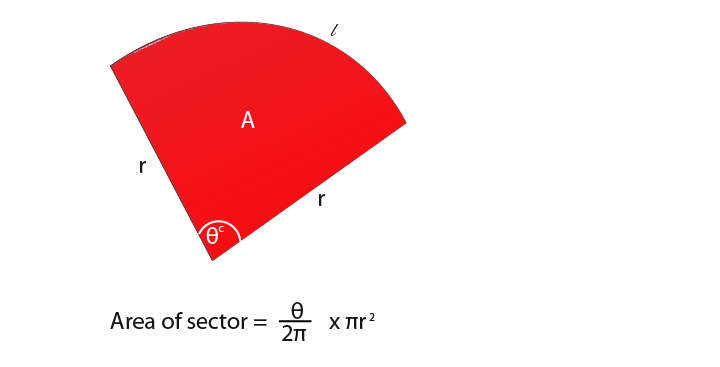
Notice that πr² is the area of a whole circle.
We can cancel out π since they exist in both parts of the equation as shown below.

We can conclude that if θ is given in radians.

Below are some examples.
Example
Find the area of the sector and arc length l

Let’s find the Arc length first, we know that;
![]()
…substitute in the known values.
![]()
…we know the sector area is;
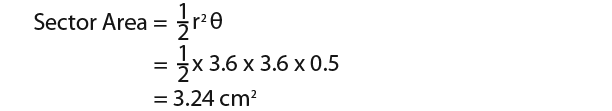
Example 2
Find the area of the sector and the arc length l
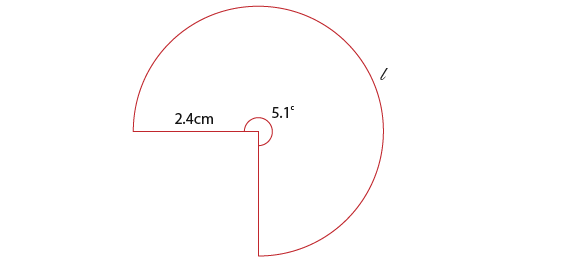
…the arc length is given by…
![]()
…therefore…

…we know the sector area is given by;
![]()
…therefore…

Area of segment
In the following we shall find the area of segment. Suppose we wanted to find the area of the segment shaded below.
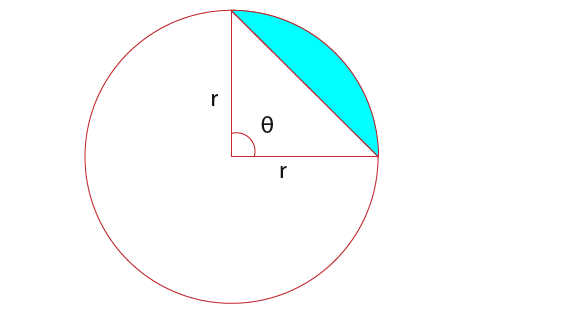
To find the area of the shaded area we first need to find the area of the sector and then take away the area of a triangle. We know the area of sector is given by;
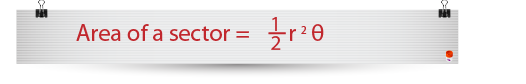
…and the area of the triangle is given by…
![]()
…so the area of the segment we’re trying to find is given by;
![]()
If instead we had to find the area of segment shaded below.
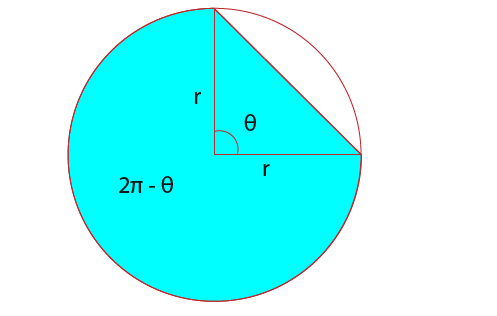
So the area of the major segment
![]()
Remember to always put the calculator into radians mode first.
Example
Find the area of the segment shaded below.
…we know area of sector is given by;
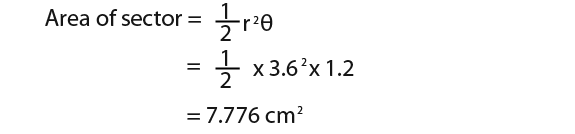
… and the area of triangle is given by…
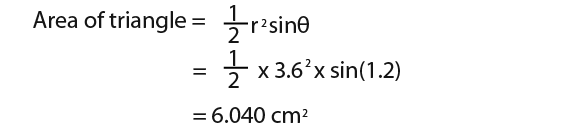
So the area of segment is;