Simultaneous equations

In this chapter we’re going to be exploring simultaneous equations.
Mr Andrews runs a coffee shop that only sells cups of coffee and cups of tea. A man one day walks into his shop and requests for 2 coffees and a cup of tea. Mr Andrews replies saying the total cost would be £1.40.
The man pays £1.40 for 2 coffees and 1 tea. We can turn this into an equation as shown below.

Suppose we wanted to find out how much Mr Andrew charge for his tea. It would be impossible to say how much he charged for his coffee and for his tea. It would be impossible to say how much he charged for coffee and for tea because there are many possibilities.
Then Mr Andrews said If you had ordered 3 coffees and a tea I would have charged you £1.70. Now we know that;

We work out the prices by looking at the differences between the two orders. The second order had one more cup of coffee which means the extra coffee in the second order cost 30p.
So if a coffee cost 30p how much is a cup of tea? Here we take one of the equations, let us take the first one.

2 coffees and a tea cost 140p.

2 coffee cost 60p.

So the tea must cost the remaining 80p. The solution we get is;

Coffee costs 30p and tea costs 80p.
The man must have paid 30p for a coffee and 80p for a tea.
Mr. Andrews one day decides to change his shop into a xylophone and yo-yo shop. One other day a woman came into the shop and asked for 2 xylophone and 3 yo-yos. Mr. Andrews replied “The total cost would be £13” We can form an equation here that shows how much 2 xylophones and 3 yo-yos cost;

Mr. Andrews then says one xylophone and one yo-yo will cost you £6. We can form an equation from this as well.

We need to look at the differences between the two possible orders or the equations that we have found. We can find out the differences by rearranging the equations like this;

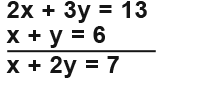
The differences between the two orders gives us another equation;

Here we still don’t know the prices since we’ve been unable to get rid of the xs or ys in the subtraction process. This is because we don’t have the same number of xs and ys in each equation.
If we double the order we would get the same number of xs as in the first order. Instead of one xylophone and one yo-yo costing £6, we shall have two of each one and pay £12. This forms the following equation.


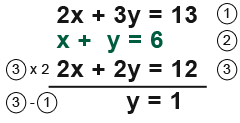
Now we substitute y=1 into equation 2;

…which means…

The solutions that we have managed to find are;

We conclude that one xylophone cost the woman £5 and one yo-yo cost the woman £1.

Proof

We can substitute the solution into one of the original equations to check whether they’re correct.

You can check this on your calculator to see whether it’s correct.
Mr. Andrews changes his business into selling fruits by opening a fruits shop. His shop sells Apples and Mangos. One day a man came into his shop and asked for 2 Apples and 3 Mangos. Mr. Andrews replied the total cost would be £1.30. We can form an equation;

Then Mr. Andrews said;

Suppose we wanted to find how much the Apples cost.
Here are the two equations that we’ll be working with.

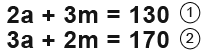
To solve this we need to get the same number of as or ms in both equations.
To make the as the same we could multiply the first equation by 1.5 which gives;

But multiplying the first equation by 1.5 gives us a decimal which adds some difficult to solve.
We could also multiply each equation by different numbers but making sure that we get the same number of equations in each equation.
Here we shall multiply equation one by 3 and equation two by 2.

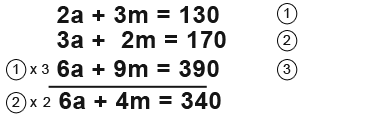
Notice we have 6as in each equation. Now we can go ahead and find the difference between equation 3 and 4.

The above is the solution for m. We can substitute m into one of the original equations to find the value or solution of a.

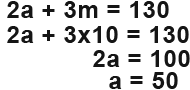
The Mangos cost 10p while the Apples cost 50p.