Sketching polynomials

This chapter explores sketching polynomials. It covers general shapes of quadratics, cubics and identifying the maximum number of turning points, roots and intercepts, and linking to factorised forms for example f(x) = (x-a)(x-b)(x-c). Before attempting this chapter you must have prior knowledge of using factorised form to sketch quadratics and find intercepts

Quadratic polynomials

A quadratic is a type of polynomial because it has x variable in it. Below is a quadratic.

We can factorise the quadratic to form;

…we know that the intercept on the y-axis would be y = c and passes through x=p and x=q on the x=axis.
Below is the graph for the quadratic.
[graph id=”13″]

Notes

So the notices to remember are if;

…the graph cuts the x-axiz at;

…and cuts y axis at;

Sketching cubics

There is also the cubic which is another type of polynomial. The simplest is y=x² you can recognise it by the S-shaped curve. For example the graph shown below is cubic.

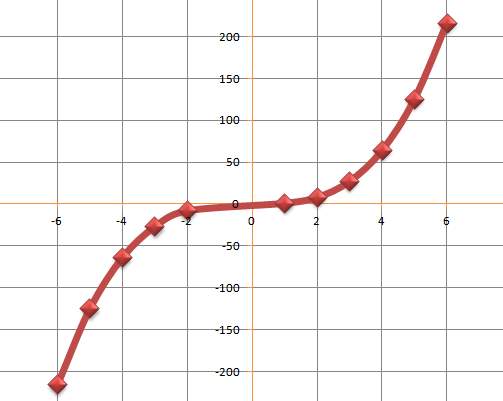
Cubics can have x² as well as x terms in them. For example;

…and…

Let us work with;

The cubic looks like the following

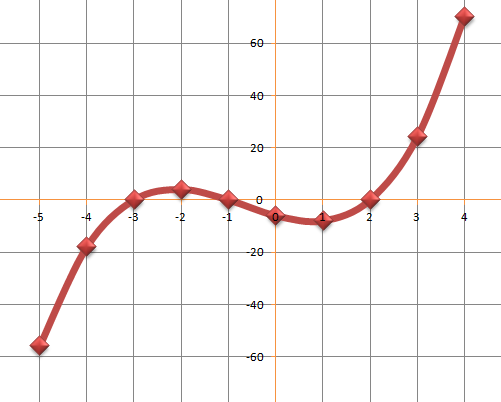
As you can see it is an S-shaped curve that crosses the graph at y=-6. The curve crosses the x-axis in 3 places. And hasa a maximum point as indicated above. These are very often referred to as turning points.
Cubics can be factorised into 3 brackets in the form;

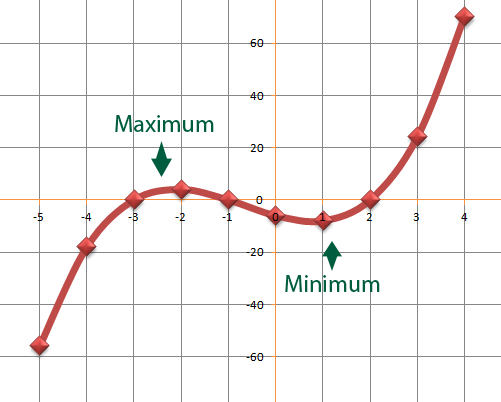
The cubic in question can be factorised to form;

Example

Here is another cubic example. Suppose we wanted to sketch the curve y=(x-1)(x-4).
The rule states that the curve goes through the x-axis when y=0. So we can substitute this where when y=0 as shown below.

This happens when x=2, x=3 and x=4. This is where it crosses the x-axis. So now we can plot the points as shown below.

Next we need to find where the curve intersects the y axis. We do that by multiplying out the last three terms in the brackets so we have;

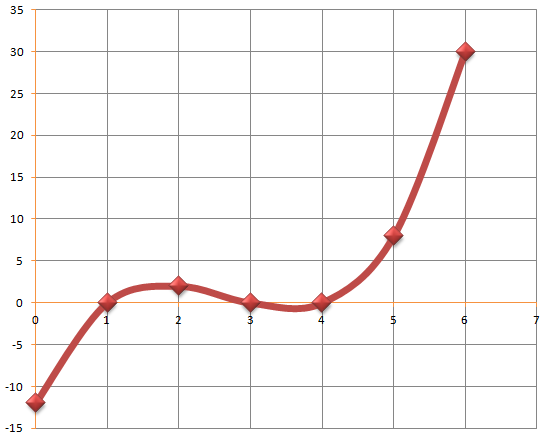
The curve crosses the y-axis at;

Repeated roots example

The following is a repeated roots example. Suppose we wanted to sketch;

We can factorise it to get;

Then we can use that to plot the points as shown below.

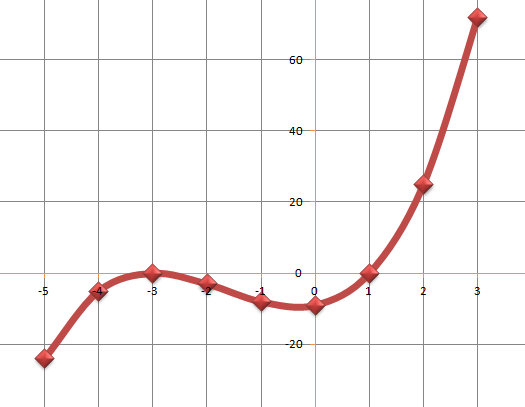
Notice that the curve crosses through -3 twice. This means that it goes through the x-axis at x=1 and touches at x=-3. This is referred to as repeated root. We find the intercept across the y-axis the same way as we did before.

The curve intecepts the y-axis at -9. The complete curve has been shown below.

Features of Polynomials

We shall start with the quadratic. Quadratics can be positive or negative for example;


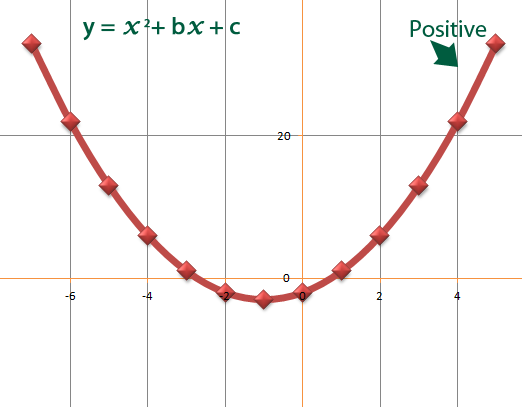
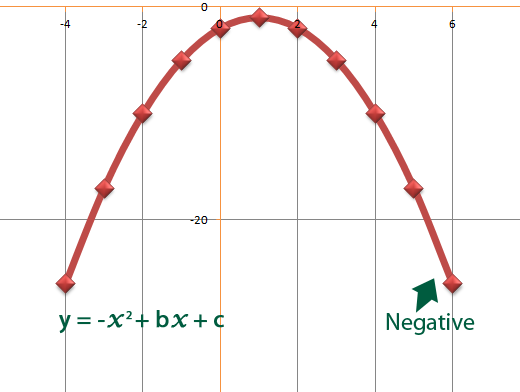
Quadratics have two roots.

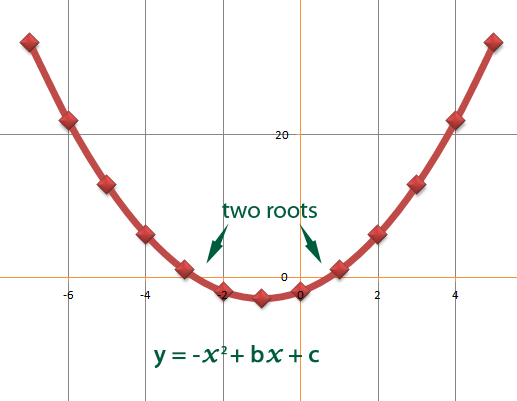
…or 1 repeated root.

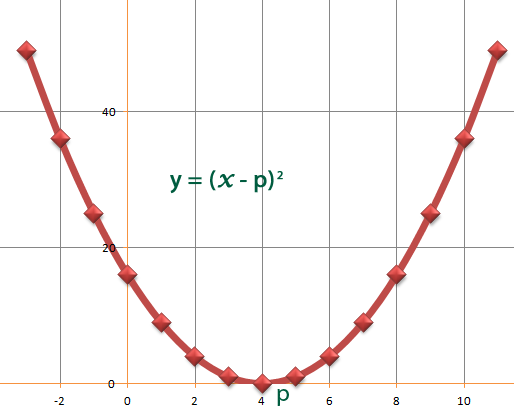
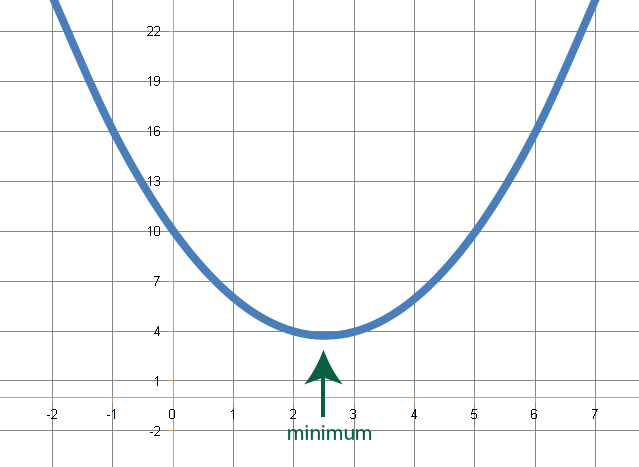
Quadratics can also have no roots at all. This is when b² – 4ac < 0. Always have just one turning point.

Cubics

Cubic can be positive as well as negative, for example;

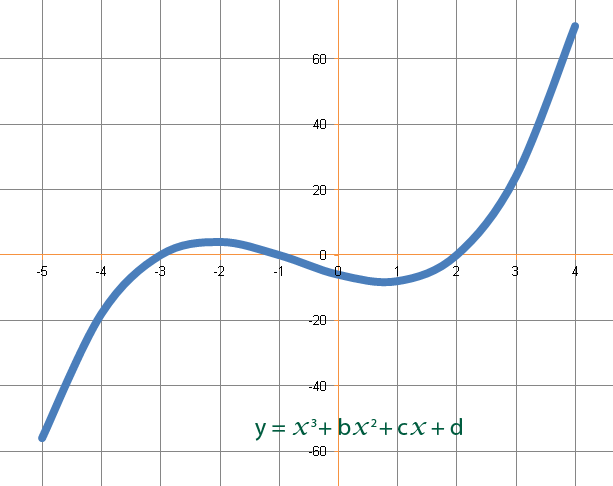
…or …

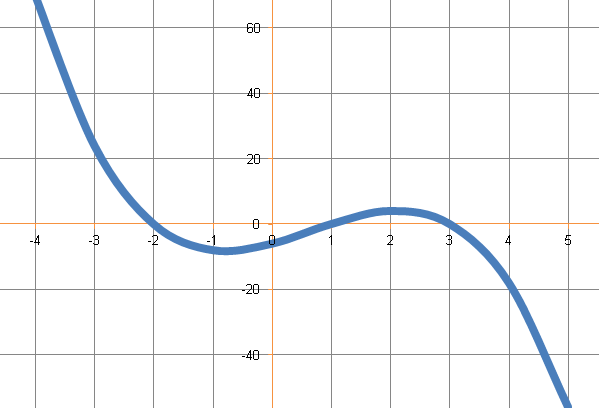
Cubics may have 3 roots marked in the form;

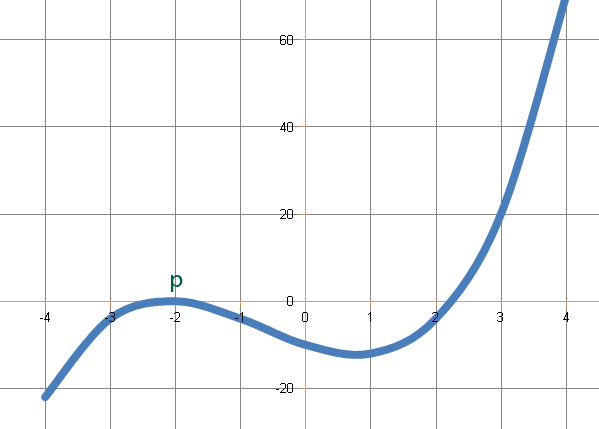
It can also have 2 roots (1 repeated) for example;

…these have been marked on the graph below;

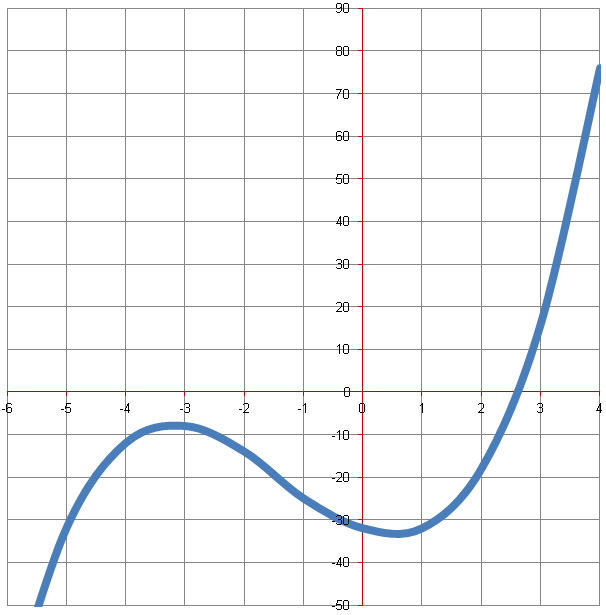
…or even just one root, for example;

…an example of one root has been marked below.

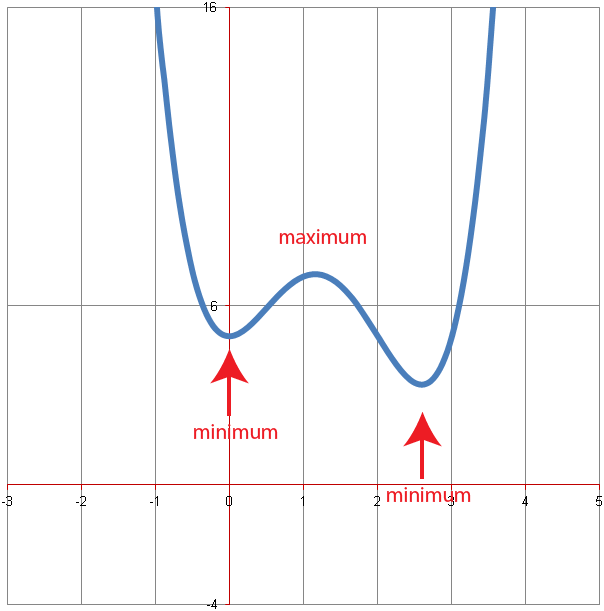
Cubics also have 2 turning points or just none.

Quartics

Quartics have an x⁴ term, quartics can be positive as well as negative for example;

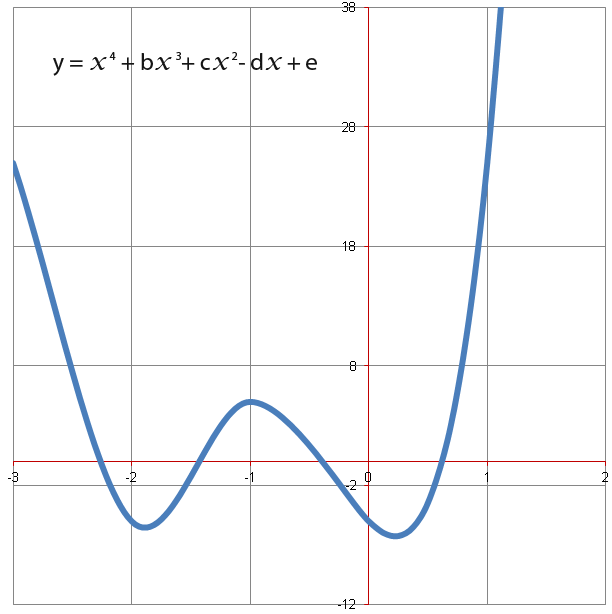
…or…

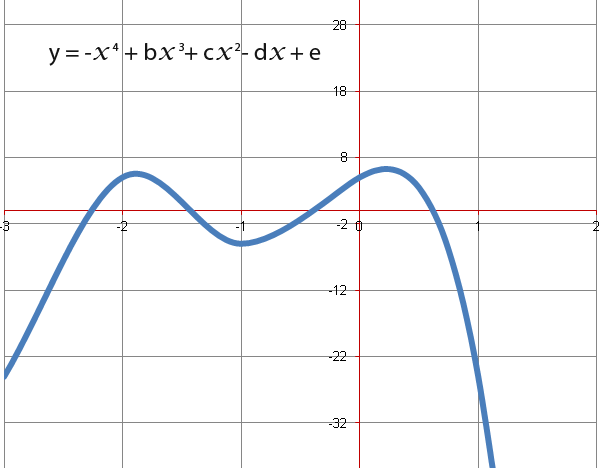
Quartics can have 4 roots for example see below;

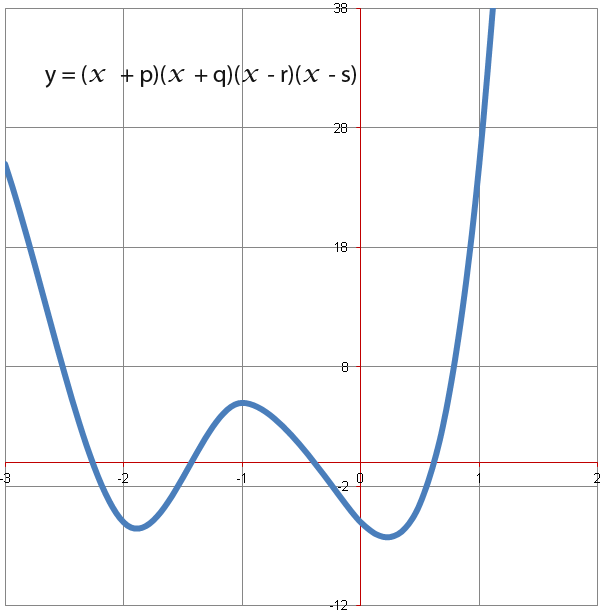
Quartics can also have just 3 roots for example.

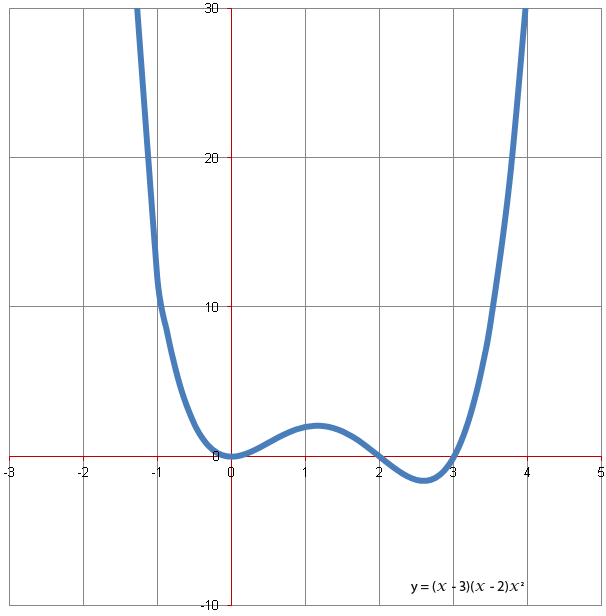
They can also have two roots for example;

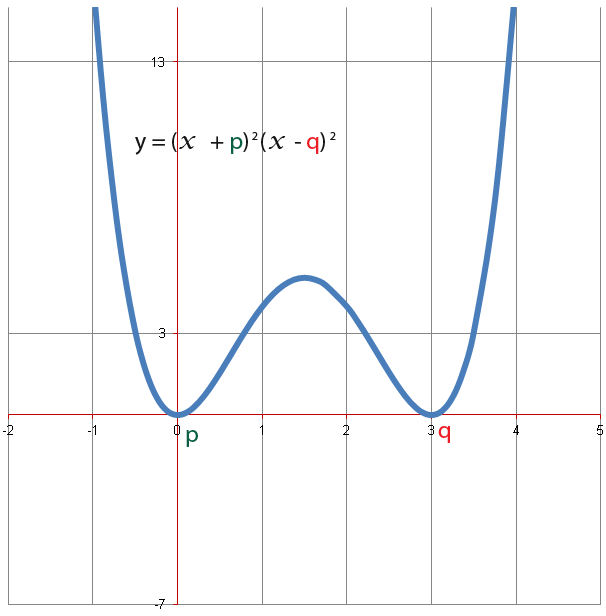
Or simply just one root;

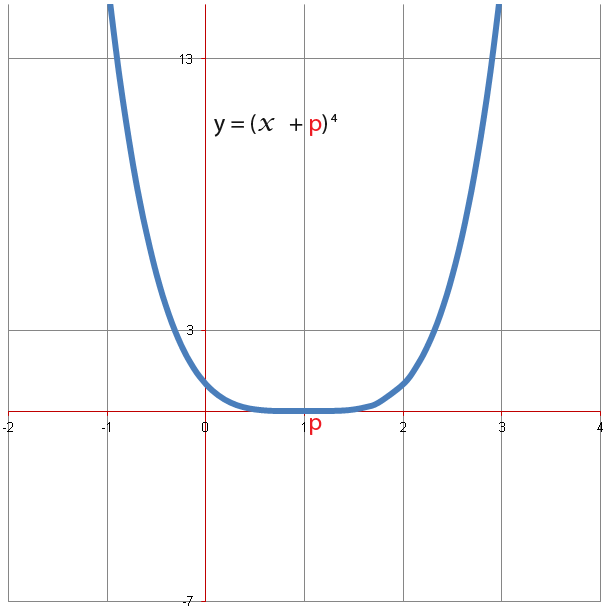
Quartics can also have no roots at all;