Sum to infinity geometric series
This is continuation from the geometric series chapter. This section explores geometric series.
To explain sum to infinity consider the following series;
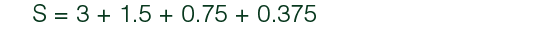
For the series above no matter how many terms of the series you add the sum never exceeds a certain number. This number is referred to as the limit of the sum or its sum to infinity. We know that a=3 and r= ½, therefore the formula for the sum to infinity is;

So the sum to infinity for this series can be given by the following equation;

We can test the sum by replacing n by different values;

In the above sums you can see that as n gets larger or as you increase the n value or use more series the sum becomes closer and closer to 6. We say that this infinite sum series is convergent, and has a sum to infinity of 6. Convergent simply means the series tends towards a specific value as more terms are added.
The sum converges because -1<r<1. The terms in the series are getting smaller. Remember that the sum to infinity of a series exists only if -1<r<1. The sum formula is;

…but if -1<r<1, r → 0 because n → ∞, therefore;
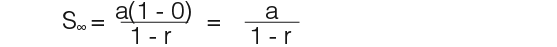
…that concludes that the sum to infinity of a geometric series is;

The above formula can only be used when -1<r<1.
Below we shall look at some examples using the sum to infinity formula;
To explain sum to infinity consider the following series;
For the series above no matter how many terms of the series you add the sum never exceeds a certain number. This number is referred to as the limit of the sum or its sum to infinity. We know that a=3 and r= ½, therefore the formula for the sum to infinity is;
So the sum to infinity for this series can be given by the following equation;
We can test the sum by replacing n by different values;

In the above sums you can see that as n gets larger or as you increase the n value or use more series the sum becomes closer and closer to 6. We say that this infinite sum series is convergent, and has a sum to infinity of 6. Convergent simply means the series tends towards a specific value as more terms are added.
The sum converges because -1<r<1. The terms in the series are getting smaller. Remember that the sum to infinity of a series exists only if -1<r<1. The sum formula is;

…but if -1<r<1, r → 0 because n → ∞, therefore;
…that concludes that the sum to infinity of a geometric series is;

The above formula can only be used when -1<r<1.
Below we shall look at some examples using the sum to infinity formula;
sum to infinity geometric series
Example:
Find the sums to infinity of the following series;
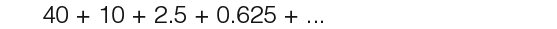
Find the sums to infinity of the following series;
Answer
Explanation In this series; a=40, r=0.25, r is between -1 and 1 therefore S∞ can be found;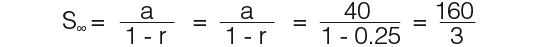
Example: The sum to 4 terms of a geometric series is 15 and the sum to infinity 16. Find the possible values of r, given that all terms are positive;
Answer
Explanation
We can form two equations here; the first involves S4 shown below;

…and the other is S∞ therefore we use the sum to infinity formula;

Now we can solve simultaneously.
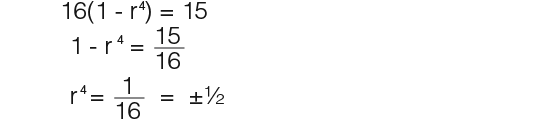
…therefore the common ratio for the series if ½.
For the second part we simply use the infinity equation and substitute r to find a;
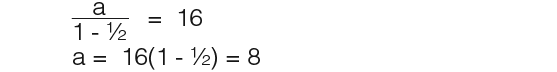
The first term in the series is 8.
We can form two equations here; the first involves S4 shown below;
…and the other is S∞ therefore we use the sum to infinity formula;
Now we can solve simultaneously.
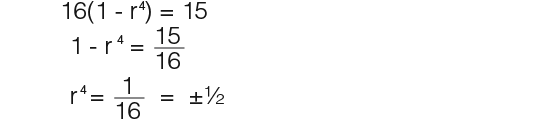
…therefore the common ratio for the series if ½.
For the second part we simply use the infinity equation and substitute r to find a;
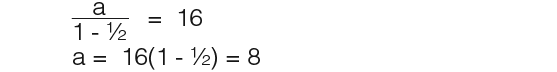
The first term in the series is 8.
