Surface Areas of Complex Shapes

This chapter explores surface areas of complex shapes. The objectives of this chapter are being able to calculate the surface areas of pyramids, cones and spheres and simple combinations of these solids. No prior knowledge is required for this chapter.

Finding the surface area of a pyramid

Suppose we wanted to find the surface area of the following square based pyramid.

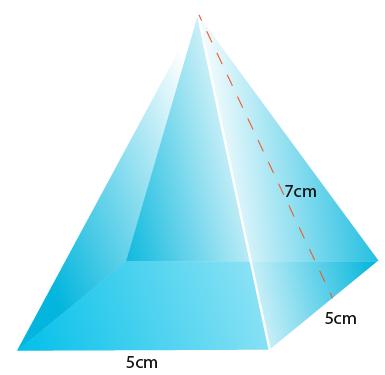
First we find the area of one of the triangular faces first, it may be useful to draw out a separate triangle as shown below;

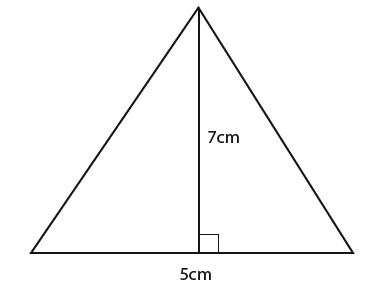
…for the triangle above we know that;

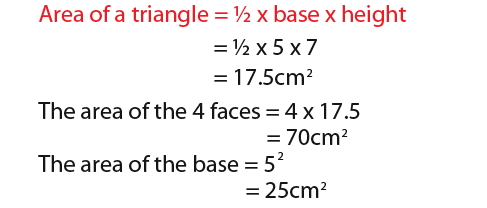
That means that the surface area is…

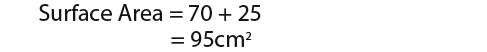
Finding the radius of a cone from its net

In this chapter section we shall explore how to find the radius of a cone from its net. Below is the net of a cone. It is the major sector of a circle radius 8. The major arc length is 31.4cm

First we draw a sketch of the cone to help work out the new radius of the base of the cone as shown below;

We know that 31.4 is the circumference of the base of the cone. Next we work out the radius;

Finding the surface area of a cone using π r l

This section explores finding the surface area of a cone using π r l. Below is a cone. It has a height of 4cm and a radius of 3cm. Suppose we wanted to find the surface area of the cone.

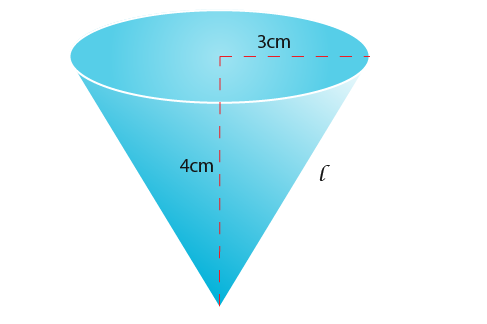
We know that the surface area is given by;

…where r is the radius of the base, and l is the slopping height.
First we need to find the value of l we do this by using ‘Pythagoras’ theorem’ It is found to be 5 cm as shown below;

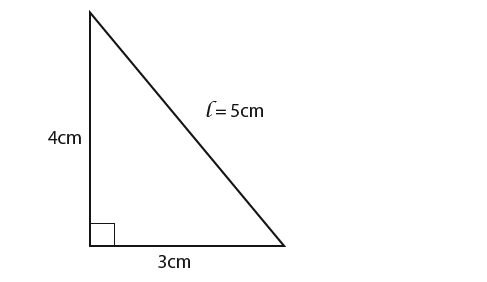
Now we know that l=5 and r=3 so we can update the diagram as shown below;

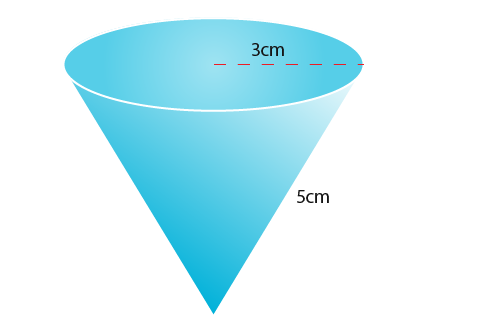
…now we can use the surface area formula;

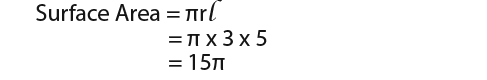
…if we include the base;

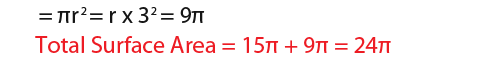
Finding the net and surface area of a frustum

This section explores finding the net and surface area of a frustum. The shape below is a frustum, it is like a lampshade.

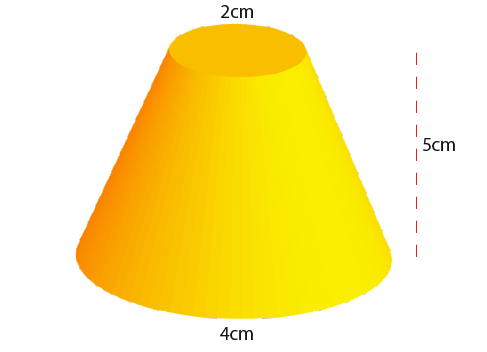
Below is how the net will look like from the shape above;

The net is horseshoe shaped it is the sector of a large circle minus the sector of a small circle. Next we shall work out the area of the next. Below is the shape again with a small cone added onto the frustum to make a bigger cone.

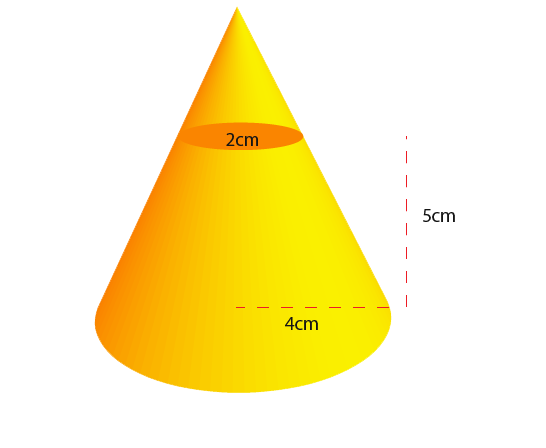
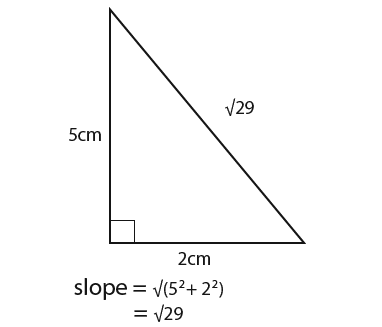
We need to find the height of the new large height. We can see that the radius goes from 4 to 2 across the height 5cm, it is doubled. That must mean that the height of the large cone must be 10cm. First we shall find out the surface area of the small cone. We know that the slope length of the small cone is the square root of 29 as shown below.

Next we find the area of a small cone as shown below;

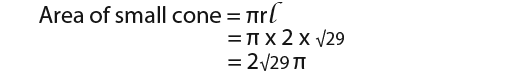
Now we can also find the area of the large cone.

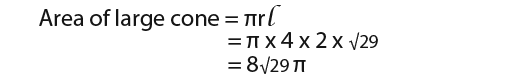
Finally we can find the surface area of the frustum.

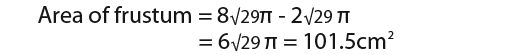
Finding the surface area of a sphere

This section offers a quick summary for finding the surface area of a sphere. Below is a sphere;

The surface area of a sphere is similar and contains the formula for the area of a circle. The formula is;