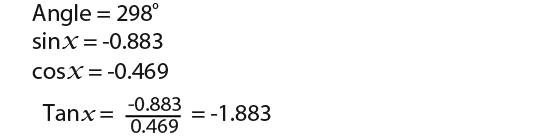Tangent graphs

This chapter explores graphs. It covers sketching the tangent graph and solving simple equations such as tan x = 0.2. Before attempting this chapter you must have prior knowledge of basic trigonometry and sine and cosine graphs.

What is the tangent of an angle?

Let us explore what a tangent is. First we draw a circle of radius 1 as shown below.

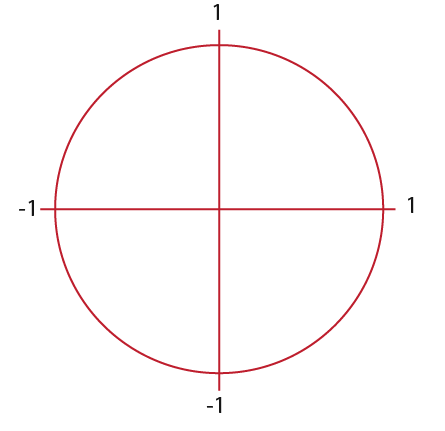
Then we draw a radius at any angle from the x-axis;

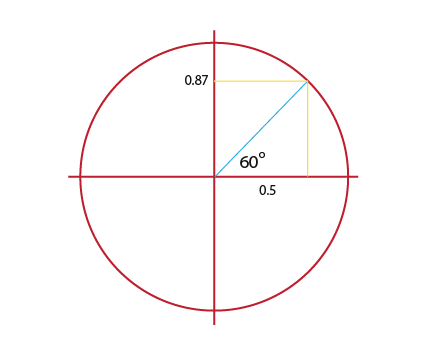
The tangent of the angle is the gradient of the line. In the case above if x = 60° then;

Example

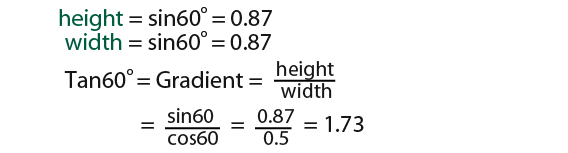
Here is another example;

Solving Tan equations

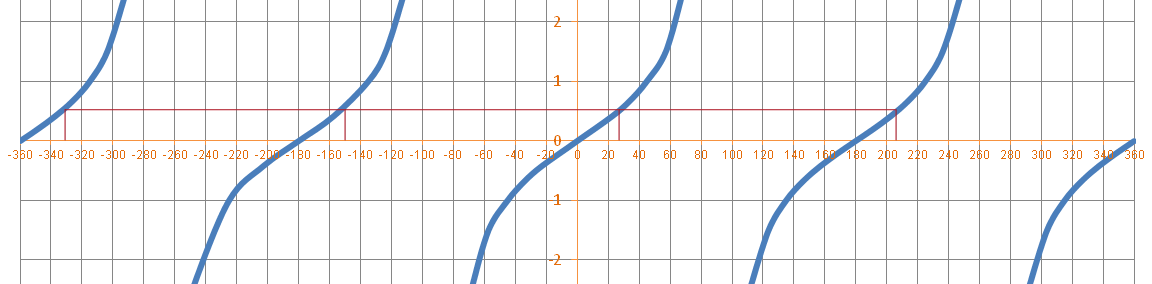
Suppose we had to solve the following equation;

The question is simply asking to write down all the angles which have a tangent of 0.5.
First use the calculator to find the first angle accuratly;

We must know that there are four angles that will have the same tangent value. We need to find all angles with the same tangent of 0.5. The other angle is;

…then…

…and…

So we can conclude that if tan x = 0.5. Then;

…the angle above have been rounded to the nearest angle. These have been shown on the tangent graph below.

Example

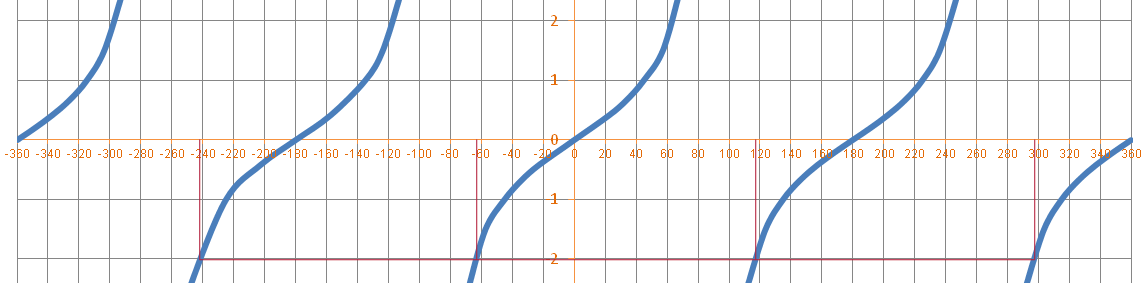
This is another example, suppose we had to solve the following;

This simply means we have to write down all the angles which have a tangent of -2.
First we use the calculator to find the first actual angle;

The other next negative angle is 63.4° beyond -180° that is;

There is also positive angles. The first positive angle is 63.4° less than 180°; so we have;

The last positive angle to find is 63.4° less than 360° that is;

So we conclude that if;

…then…

The angles have been rounded to the nearest degree. The angles have been shown on the graph below.