Trigonometric Equations 2

This chapter explores trigonometric equations. It covers solving harder trigonometric equations using identities. Before attempting this chapter you must have prior knowledge of solving trigonometric equations and must go through trigonometric equations 1

Solving sin x = 1/4

Suppose we had to solve the following equation.

…in the range -180° ≤ x ≤ 180°
To simplify we square root both sides to get;

There is a positive and a negative that must mean;

…we need to use both equations. The solutions for;

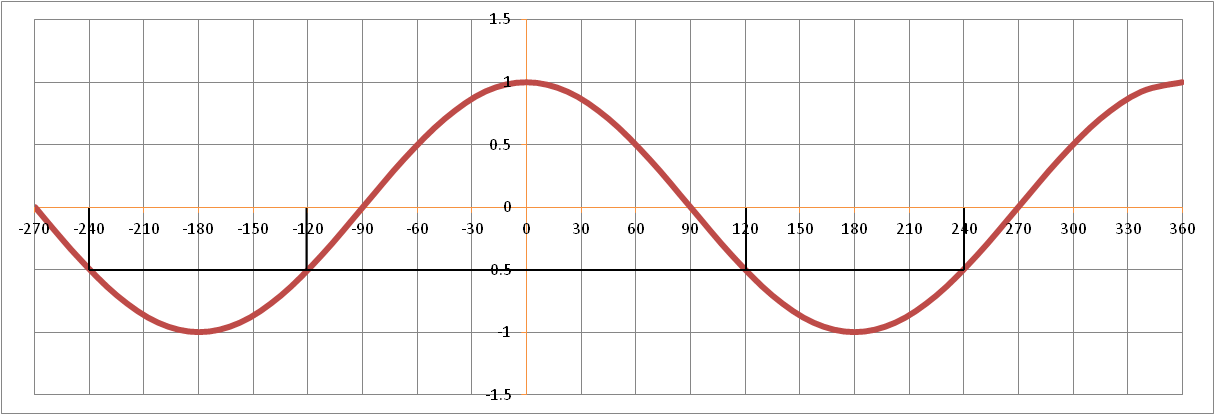
…have been shown on the graph below;

…we see;

And below shows the solutions for;


…we see

So the solutions are;

Solving cosx – cosx = 0

Suppose we wanted to solve the following equation;

…in the range of 0° ≤ x ≤ 360°
First we factorise by taking out cosx as the common factor.

So we have two solutions either.

or

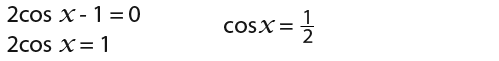
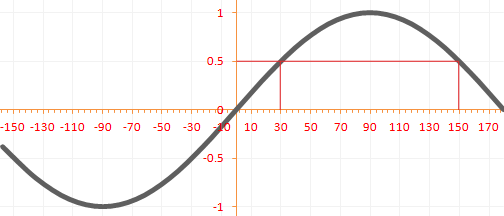
For cosx = 0 we have;

…we have;

…and for;

…we have…

So the solutions are;

Solving 3sinx = 4cosx

Suppose we wanted to solve the following equation;

…in the range of 0° ≤ x ≤ 360°
The equation involves sin θ and cos θ. That is why it looks difficult. We can simplify it by using the identity.

…so now we have…
[IMAGE]
…we know that;

…now we have;

The solutions have been shown on the graph below.

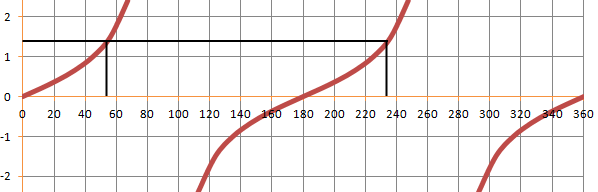
To find the first angle accurately we use;

The second angle is;

The solutions are;

Solving 2 sinx + tan x = 0

Suppose we had to solve;

…in the range -360° ≤ x ≤ 360°
Again we use the identity;

…simplify it to get;

…then we multiply through by cos θ to get;

Now we factorise by taking out sin θ as the common factor.

So we have 2 solutions;

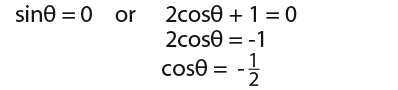
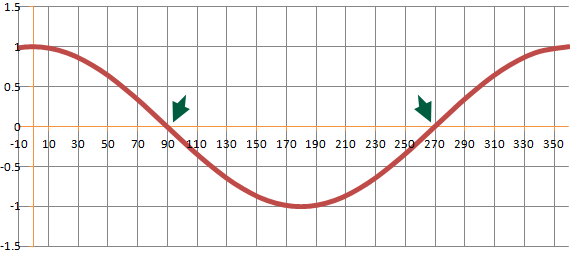
For sinθ = 0 we have;

…and for cosθ = -1/2 we have…

…these are shown on the graph below.

Solving 2sinx = 3cosx

Suppose we had to solve;

…in the range of 0° ≤ x ≤ 360°
We could try to divide through to get;

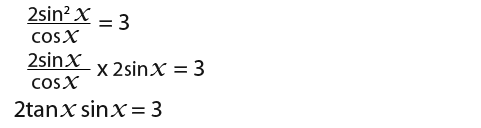
The above would not help because we still have a spare sinx. So again we have to start again… Let us use the following instead;

…that must mean that;

We can substitute this into the original equation as shown below;

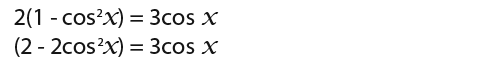
Let’s turn the equation in an obvious quadratic equation by taking every term to the right.

Above we have a quadratic equation with cosx. Let us look at the equation like the following where y=cosx

For the equation above we can factorise it as shown below;

For the original equation that must mean;

Now we can solve when;

For;

…there are no solutions.
So the answer is;

We can check this, let us try 60° in the original formula;

Solving 1+cosx = 3sinx

In this section we shall solve the following equation;

…for 0° ≤ x ≤ 360°
Let us substitute sin²x by using the following;

So we have;

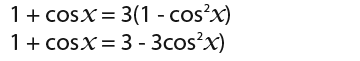
We take everything onto the left hand side as shown below;

Like we did before we think about this like the following where y=cosx

We factorise our assumption.

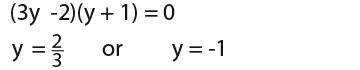
So we can relate the above to the original equation;

We can now solve for both solutions when;

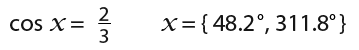
…and…

So the final answer becomes;

Solving 2cos2x + 3sinx = 3

In this section we shall be solving the following equation.

…for -180° ≤ x ≤ 180°
The above equation appears to e complex because it has 2 θ instead of just θ. Let us replace θ with x to get;

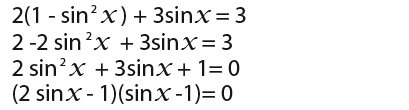
So we have;
[]
…actually what we have is the following since we replaced θ with x.

Let us first solve for;

Remember we need to find the solutions between -360° and 360°. The angles are;

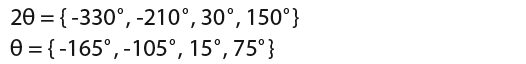
Now we can solve for;

The angles are;

So the final solutions are;

You can choose any of the angles to see whether this is correct.