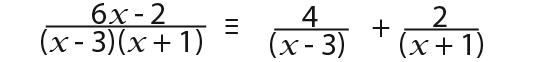Two linear factors in the denominator of partial fractions

This article is a continuation from the previous article. I recommend reading through it before attempting this. This article explores partial fractions with two linear factors in the denominator.
We can split fractions with two linear fractions in the denominator into partial fractions. In the previous article we saw where a partial fraction was put into a single fraction. So we can split a single fraction such as;

…into partial fractions;

In general an expression with two linear terms in the denominator such as;

…can be split into partial fractions of the term;

…where A and B are constants.
In this article we shall look at two methods of doing this; by substitution and by equating coefficients.

Example

In this example we shall split the following fraction into partial fractions – first by substitution and then by equating coefficients;

By Substitution

First we shall use the substitution method; To do this we set the expression above identical to;

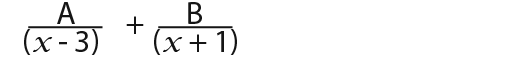
…that is;

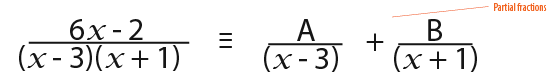
Now we must solve to find the value of A and B. We can simplify further;

To find the values of A and B at this point we simply equal the numerators to each other because the two expressions are an equivalence relation;

To find A an B we test the expression by substituting in different values for x.
To find A we substitute in x = 3 to get;

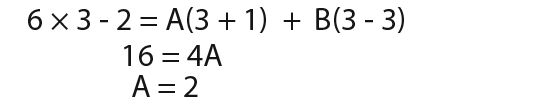
We find that A = 4.
To find B we substitute in x=-1 to get;

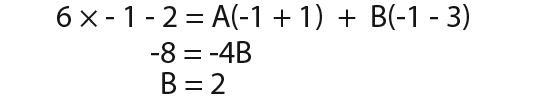
So substituting in the values of A and B that we have found we get;

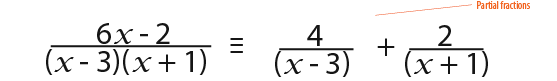
By equating coefficients

Now we shall use the equating coefficients methods. Again as we did before;

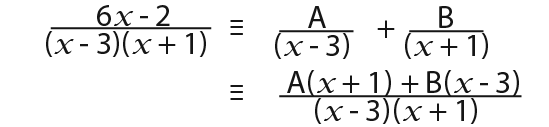
Again because it is an equivalence relation we set the numerators equal to each other.

Now we simply expand the brackets and equate the coefficients;

…then collect like terms;

Now we can equate the coefficients of x’s in the expression;

…we can also equate the constant terms;

To find the values of A and B we solve simultaneously. We find that;

…and;

So now we just replace A and B in the partial fractions;